题目内容
如图所示，放置在竖直平面内的光滑杆AB，是按照从高度为h处以初速度v平抛的运动轨迹制成的，A端为抛出点，B端为落地点．现将一小球套于其上，由静止开始从轨道A端滑下．已知重力加速度为g，当小球到达轨道B端时（ ）
A．小球的速率为
B．小球的速率为
C．小球在水平方向的速度大小为v
D．小球在水平方向的速度大小为
【答案】分析：小球在光滑杆上只有重力做功，故机械能守恒，由机械能守恒定律可求得小球到达B点时的速度；由平抛运动的规律可求得B点切线与水平方向的夹角； 再由运动的合成与分解可求得小球在最低点水平方向的速度．
解答：解：由机械能守恒定律，mgh=
mv2，解得小球到达轨道B端时速率为v=
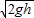；故A错误，B正确；
当小球滑到B点时，设小球的速度与水平方向间的夹角为θ，则tanθ=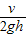
，cosθ=
；
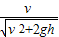小球在水平方向的速度v=vcosθ=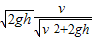
；
故C错误，D正确；
故选BD．
点评：本题通过平抛运动的速度方向关系考查运动的合成与分解，注意小球做的是初速度为零的匀加速直线运动．
解答：解：由机械能守恒定律，mgh=
mv2，解得小球到达轨道B端时速率为v=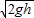；故A错误，B正确；当小球滑到B点时，设小球的速度与水平方向间的夹角为θ，则tanθ=
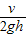，cosθ=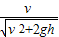；小球在水平方向的速度v=vcosθ=
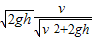； 故C错误，D正确；
故选BD．
点评：本题通过平抛运动的速度方向关系考查运动的合成与分解，注意小球做的是初速度为零的匀加速直线运动．
练习册系列答案
相关题目
如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上．滑轨由四部分粗细均匀的滑杆组成：水平直轨道AB；倾斜直轨道CD，长L=6m，与水平面间的夹角θ=370；半径R1=1m的圆弧轨道APC；半径R2=3m的圆弧轨道BQED．直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点．倾斜直轨道CD与小球间的动摩擦因数为μ=5/32，其余部分均为光滑轨道，取g=10m/s2，sin37°=0.6，cos37°=0.8．现让小球从AB的正中央以初速度V0=10m/s开始向左运动，问：
（2010?上海模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以初动能Ek0从B点开始沿BA向上运动，小球与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，AB、CD与两圆弧形轨道相切，BQC的半径为r=1m，APD的半径为R=2m，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=
如图所示，放置在竖直平面内的光滑曲线轨道OA足够长，它是按照从坐标原点O处以初速度v0作平抛运动的轨迹制成的．现将一小球套于其上，从O点由静止开始沿轨道下滑．已知重力加速度为g，则小球的速度v与水平方向的位移x关系是v=