题目内容
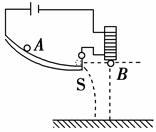
如图，一小球从一半圆轨道左端A点正上方某处开始做平抛运动（小球可视为质点），飞行过程中恰好与半圆轨道相切于B点。O为半圆轨道圆心，半圆轨道半径为R，OB与水平方向夹角为60°，重力加速度为g，则小球抛出时的初速度为
A． | B． |
C． | D． |
A
解析试题分析：平抛运动经过B点时，合速度沿切线方向，速度合成如下图，几何关系可知
，竖直方向自由落体运动，根据几何关系可得水平方向的位移
，带入可得
，整理得
，那么水平速度
，对照选项A对。
考点：平抛运动
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
如图所示，x轴在水平地面上，y轴竖直向上，在y轴上的P点分别沿x轴正方向和y轴正方向以相同大小的初速度抛出两个小球a和b，不计空气阻力，若b上行的最大高度等于P点离地的高度，则从抛出到落地，有
A．a的运动时间是b的运动时间的 倍 |
| B．a的位移大小是b的位移大小的倍 |
| C．a、b落地时的速度相同，因此动能一定相同 |
| D．a、b落地时的速度不同，但动能可能相同 |
在空中某一高度将一小球水平抛出，取抛出点为坐标原点，初速度方向为
轴正方向，竖直向下为
轴正方向，得到其运动的轨迹方程为
（
为已知量），重力加速度为
，则根据以上条件可以求得
| A．物体距离地面的高度 |
| B．物体作平抛运动的初速度 |
| C．物体落地时的速度 |
| D．物体在空中运动的总时间 |
的速度水平抛出，在落地之前经过空中A、B两点．在A点小球速度方同与水平方同的夹角为
．在B点小球速度方同与水平方同的夹角为
（空气阻力忽略不计．g取
）．以下判断中正确的足
如图所示，一网球运动员将球在边界处正上方正对球网水平向前击出，球刚好过网落在图中位置（不计空气阻力），相关数据如图，下列说法中正确的是 ( )
| A．击球点高度h1与球网高度h2之间的关系为h1 =1.8h2 |
B．若保持击球高度不变，球的初速度满足 ，一定落在对方界内 |
| C．任意降低击球高度（仍大于h2），只要击球初速度合适，球一定能落在对方界内 |
| D．任意增加击球高度，只要击球初速度合适，球一定能落在对方界内 |
如图所示，ab为竖直平面内的半圆环acb的水平直径，c为环上最低点，环半径为R。将一个小球从a点以初速度
沿ab方向抛出。设重力加速度为g，不计空气阻力。
A．当小球的初速度 时，掉到环上时的竖直分速度最大 |
B．当小球的初速度 时，将撞击到环上的圆弧ac段‘ |
| C．当取适当值，小球可以垂直撞击圆环 |
| D．无论取何值，小球都不可能垂直撞击圆环 |
如图所示，在一次空地演习中，离地H高处的飞机以水平速度
发射一颗炮弹欲轰炸地面目标P，反应灵敏的地面拦截系统同时以速度
竖直向上发射炮弹拦截. 设拦截系统与飞机的水平距离为s，若拦截成功，不计空气阻力，则、的关系应满足
| A．= | B．= |
C．= | D．= |
如图所示，将一质量为m的小球从空中O点以速度v0水平抛出，飞行一段时间后，小球经过空间P点时动能为Ek ，不计空气阻力，则
A．小球经过P点时竖直分速度为 |
B．从O点到P点，小球的高度下降 |
C．从O点到P点过程中，小球运动的平均速度为 |
D．从O点到P点过程中，小球运动的平均速度为 |