��Ŀ����
 ��ˮƽ�������˶���С������ײ���һ����Ϊm1��ľ�飬ľ��ͳ���ͨ��һ��ˮƽ�ᵯ�������ӣ����ɵľ���ϵ��Ϊk���ڳ���Ķ�����һ��ϸ������һ����Ϊm2��С��ij��ʱ���ڷ���ϸ������ֱ����ļн�Ϊ�ȣ������ʱ����ľ���복��Ҳ������Ծ�ֹ����ͼ��ʾ������ľ���복��ײ���Ħ�������������ʱ���ڵ��ɵ��α���x��ϸ�߶�С�������T��
��ˮƽ�������˶���С������ײ���һ����Ϊm1��ľ�飬ľ��ͳ���ͨ��һ��ˮƽ�ᵯ�������ӣ����ɵľ���ϵ��Ϊk���ڳ���Ķ�����һ��ϸ������һ����Ϊm2��С��ij��ʱ���ڷ���ϸ������ֱ����ļн�Ϊ�ȣ������ʱ����ľ���복��Ҳ������Ծ�ֹ����ͼ��ʾ������ľ���복��ײ���Ħ�������������ʱ���ڵ��ɵ��α���x��ϸ�߶�С�������T����������С��Ϊ�о��������������������ţ�ٵڶ�����������ٶȣ���ΪС���ļ��ٶȣ������ϸ�߶�С�������T���ٶ�����Ϊm1��ľ���о�������ţ�ٵڶ����ɺͺ��˶���������ɵ��α���x��
����⣺��С��Ϊ�о��������������������ţ�ٵڶ����ɵ�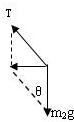 ��
��
m2gtan��=m2a���ã�a=gtan��
T=
��������Ϊm1��ľ��Ϊ�о�������ţ�ٵڶ����ɵ�
F=m1a
���ɺ��˶��ɵã�F=kx
���x=
�𣺵��ɵ��α���Ϊ
��ϸ�߶�С�������Ϊ
��
 ��
��m2gtan��=m2a���ã�a=gtan��
T=
| m2g |
| cos�� |
��������Ϊm1��ľ��Ϊ�о�������ţ�ٵڶ����ɵ�
F=m1a
���ɺ��˶��ɵã�F=kx
���x=
| m1gtan�� |
| k |
�𣺵��ɵ��α���Ϊ
| m1gtan�� |
| k |
| m2g |
| cos�� |
����������Ҫץסľ����С���ļ��ٶȶ���ͬ�����ѡ���о������ø��뷨������

��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ
 ��ͼ��ʾ���ֲ�ˮƽ������뾶ΪR�Ĺ⻬��Բ���BCD�����ӣ�����ͬһ��ֱƽ���ڣ�O��BCD��Բ�ģ�BOD��ͬһ��ֱ���ϣ�����Ϊm��С�����ˮƽ����F�������£��ɾ�ֹ��ʼ���ȼ���ֱ���˶���С�����ˮƽ�����Ķ�Ħ������Ϊ�̣���С����˶���B��ʱ��ȥF��С����ذ�Բ����˶�ǡ����ͨ��D�㣮��
��ͼ��ʾ���ֲ�ˮƽ������뾶ΪR�Ĺ⻬��Բ���BCD�����ӣ�����ͬһ��ֱƽ���ڣ�O��BCD��Բ�ģ�BOD��ͬһ��ֱ���ϣ�����Ϊm��С�����ˮƽ����F�������£��ɾ�ֹ��ʼ���ȼ���ֱ���˶���С�����ˮƽ�����Ķ�Ħ������Ϊ�̣���С����˶���B��ʱ��ȥF��С����ذ�Բ����˶�ǡ����ͨ��D�㣮�� ��2008?�˱�ģ�⣩��ͼ��ʾ����L=1m����h=7.2m������M=8kg���ϱ���⻬��ľ����ˮƽ�������˶���ľ��������Ķ�Ħ��������=0.2����ľ����ٶ�Ϊvo=3m/sʱ����һ����m=2kg�Ĺ⻬С���飨����Ϊ�ʵ㣩���������ľ���ϱ�����Ҷˣ�ȡg=10m/s2����
��2008?�˱�ģ�⣩��ͼ��ʾ����L=1m����h=7.2m������M=8kg���ϱ���⻬��ľ����ˮƽ�������˶���ľ��������Ķ�Ħ��������=0.2����ľ����ٶ�Ϊvo=3m/sʱ����һ����m=2kg�Ĺ⻬С���飨����Ϊ�ʵ㣩���������ľ���ϱ�����Ҷˣ�ȡg=10m/s2����
