题目内容
1. 如图所示是半径R=5cm的透明圆柱体的横截面,圆柱体的折射率为n=$\sqrt{3}$,一束平行于直径AB的光线从D点射入圆柱体,折射光线恰好通过B点,求光在圆柱体中传播的时间.
如图所示是半径R=5cm的透明圆柱体的横截面,圆柱体的折射率为n=$\sqrt{3}$,一束平行于直径AB的光线从D点射入圆柱体,折射光线恰好通过B点,求光在圆柱体中传播的时间.
分析 光在介质中的速度v=$\frac{c}{n}$,作出光路图,由几何知识分析得到,入射角等于折射角的2倍,由折射定律求出入射角.由数学知识求解入射点D到B间的距离d,由$t=\frac{d}{v}$求出时间.
解答  解:光在透明体中的传播速度v=$\frac{c}{n}$=$\frac{3.0×1{0}^{8}}{\sqrt{3}}$m/s=1.73×108m/s
解:光在透明体中的传播速度v=$\frac{c}{n}$=$\frac{3.0×1{0}^{8}}{\sqrt{3}}$m/s=1.73×108m/s
光线经折射后经过D点后光路图如图所示.
由折射定律得 n=$\frac{sini}{sinr}$,
又由几何关系得:i=2r,
代入解得:i=60°
所以光线在圆柱体中传播的距离:d=2Rcos r=5×cos30°=$\frac{5\sqrt{3}}{2}$cm
光在圆柱体中传播的时间:t=$\frac{d}{v}$
代入数据得:t=5×10-10s.
答:光在圆柱体中的传播的时间为5×10-10s.
点评 本题是折射定律与v=$\frac{c}{n}$的综合应用,关键是画出光路图,运用几何知识求解入射角与折射角.

练习册系列答案
相关题目
9. 某同学设计了一个测定列车加速度的仪器,如图所示,图中AB是一段半径为r 的四分之一圆弧形的合金轨道(其电阻不可忽略,横截粗细均匀),其A点切线竖直、B点切线水平,O为圆心;用长为r、电阻不计的柔软金属导线线将一个可视为质点的金属球悬挂在O点,金属球恰好与轨道良好接触且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,并串入了一个理想电流表
某同学设计了一个测定列车加速度的仪器,如图所示,图中AB是一段半径为r 的四分之一圆弧形的合金轨道(其电阻不可忽略,横截粗细均匀),其A点切线竖直、B点切线水平,O为圆心;用长为r、电阻不计的柔软金属导线线将一个可视为质点的金属球悬挂在O点,金属球恰好与轨道良好接触且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,并串入了一个理想电流表 ,O、B间还接有一个理想电压表
,O、B间还接有一个理想电压表 ,整个装置安装在与列车前进的方向平行的竖直平面内.下列说法中正确的是( )
,整个装置安装在与列车前进的方向平行的竖直平面内.下列说法中正确的是( )
 某同学设计了一个测定列车加速度的仪器,如图所示,图中AB是一段半径为r 的四分之一圆弧形的合金轨道(其电阻不可忽略,横截粗细均匀),其A点切线竖直、B点切线水平,O为圆心;用长为r、电阻不计的柔软金属导线线将一个可视为质点的金属球悬挂在O点,金属球恰好与轨道良好接触且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,并串入了一个理想电流表
某同学设计了一个测定列车加速度的仪器,如图所示,图中AB是一段半径为r 的四分之一圆弧形的合金轨道(其电阻不可忽略,横截粗细均匀),其A点切线竖直、B点切线水平,O为圆心;用长为r、电阻不计的柔软金属导线线将一个可视为质点的金属球悬挂在O点,金属球恰好与轨道良好接触且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,并串入了一个理想电流表 ,O、B间还接有一个理想电压表
,O、B间还接有一个理想电压表 ,整个装置安装在与列车前进的方向平行的竖直平面内.下列说法中正确的是( )
,整个装置安装在与列车前进的方向平行的竖直平面内.下列说法中正确的是( )| A. | 从图中看到列车一定是向右加速运动 | |
| B. | 当列车的加速度增大时,电压表 的读数减小 的读数减小 | |
| C. | 当列车的加速度增大时,电流表 的读数增大 的读数增大 | |
| D. | 若电压表显示3 V,则列车的加速度为$\frac{\sqrt{3}}{3}$g |
16.“北斗”导航系统是我国自行研发的全球导航系统.导航系统中有5颗地球同步卫星,若月球公转周期约为27天,则导航系统中同步卫星与月球( )
| A. | 角速度之比约为1:27 | B. | 线速度之比约为3:1 | ||
| C. | 向心加速度之比约为27:1 | D. | 半径之比约为1:3 |
13.下列说法中正确是( )
| A. | 气体对容器壁有压强是气体分子对容器壁频繁碰撞的结果 | |
| B. | 物体温度升高,组成物体的所有分子速率均增大 | |
| C. | 一定质量的理想气体等压膨胀过程中气体一定从外界吸收热量 | |
| D. | 自然发生的热传递过程是向着分子热运动无序性增大的方向进行的 | |
| E. | 饱和汽压与分子密度有关,与温度无关 |
10.物理学发展的过程中,许多物理学家的科学发现推动了人类历史的进步.对以下几位物理学家所作科学贡献的表述中,与事实不相符的是( )
| A. | 伽利略根据理想斜面实验,提出了力不是维持物体运动的原因 | |
| B. | 亚里士多德认为两个从同一高度自由落下的物体,重的物体与轻的物体下落一样快 | |
| C. | 牛顿发现了万有引力定律,卡文迪许比较准确地测出了引力常量G | |
| D. | 法拉第提出了场的概念并用电场线形象地描述电场 |
11. 如图所示,空间存在一水平向的匀强电场和一水平方向的匀强磁场,磁场的磁感应强度大小为B,电场强度大小为$E=\frac{{\sqrt{3}mg}}{q}$,电场方向和磁场方向相互垂直.在此电磁场正交的空间中有一足够长的固定粗糙绝缘杆,与电场正方向成60°夹角且处于竖直平面内.一质量为m,带电量为+q的小球套在绝缘杆上.若给小球一沿杆向下的初速度v0,小球恰好做匀速运动,且小球电量保持不变,重力加速度为g,则下列说法正确的是( )
如图所示,空间存在一水平向的匀强电场和一水平方向的匀强磁场,磁场的磁感应强度大小为B,电场强度大小为$E=\frac{{\sqrt{3}mg}}{q}$,电场方向和磁场方向相互垂直.在此电磁场正交的空间中有一足够长的固定粗糙绝缘杆,与电场正方向成60°夹角且处于竖直平面内.一质量为m,带电量为+q的小球套在绝缘杆上.若给小球一沿杆向下的初速度v0,小球恰好做匀速运动,且小球电量保持不变,重力加速度为g,则下列说法正确的是( )
 如图所示,空间存在一水平向的匀强电场和一水平方向的匀强磁场,磁场的磁感应强度大小为B,电场强度大小为$E=\frac{{\sqrt{3}mg}}{q}$,电场方向和磁场方向相互垂直.在此电磁场正交的空间中有一足够长的固定粗糙绝缘杆,与电场正方向成60°夹角且处于竖直平面内.一质量为m,带电量为+q的小球套在绝缘杆上.若给小球一沿杆向下的初速度v0,小球恰好做匀速运动,且小球电量保持不变,重力加速度为g,则下列说法正确的是( )
如图所示,空间存在一水平向的匀强电场和一水平方向的匀强磁场,磁场的磁感应强度大小为B,电场强度大小为$E=\frac{{\sqrt{3}mg}}{q}$,电场方向和磁场方向相互垂直.在此电磁场正交的空间中有一足够长的固定粗糙绝缘杆,与电场正方向成60°夹角且处于竖直平面内.一质量为m,带电量为+q的小球套在绝缘杆上.若给小球一沿杆向下的初速度v0,小球恰好做匀速运动,且小球电量保持不变,重力加速度为g,则下列说法正确的是( )| A. | 小球的初速度为${v_0}=\frac{2mg}{qB}$ | |
| B. | 若小球的初速度为$\frac{3mg}{qB}$,小球将做加速度不断增大的减速运动,最后停止 | |
| C. | 若小球的初速度为$\frac{mg}{qB}$,小球将做加速度不断增大的减速运动,最后停止 | |
| D. | 若小球的初速度为$\frac{mg}{qB}$,则运动中克服摩擦力做功为$\frac{{{m^3}{g^2}}}{{2{q^2}{B^2}}}$ |
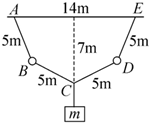 如图所示,AB、BC、CD和DE为质量可忽略的等长细线,长度均为5m,A、E端悬挂在水平天花板上,AE=14m,B、D是质量均相同的小球.质量为18千克的重物挂于C点,平衡时C点离天花板的垂直距离为7m,试求小球B、D的质量.
如图所示,AB、BC、CD和DE为质量可忽略的等长细线,长度均为5m,A、E端悬挂在水平天花板上,AE=14m,B、D是质量均相同的小球.质量为18千克的重物挂于C点,平衡时C点离天花板的垂直距离为7m,试求小球B、D的质量. 如图所示,质量为4kg的物体在100N水平推力作用下,(g取10m/s2)
如图所示,质量为4kg的物体在100N水平推力作用下,(g取10m/s2) 风筝(图甲)借助于风对其均匀的作用力和牵线对它的拉力作用,才得以在空中处于平衡状态.如图乙,风筝平面AB与地面夹角为30°,牵线与风筝面夹角为53°,风筝质量为300g,求风对风筝的作用力的大小.(风对风筝的作用力与风筝平面垂直,g取10m/s2)
风筝(图甲)借助于风对其均匀的作用力和牵线对它的拉力作用,才得以在空中处于平衡状态.如图乙,风筝平面AB与地面夹角为30°,牵线与风筝面夹角为53°,风筝质量为300g,求风对风筝的作用力的大小.(风对风筝的作用力与风筝平面垂直,g取10m/s2)