题目内容
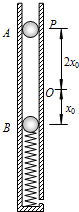 质量为m的小球B与质量为2m的小球C之间用一根轻质弹簧连接,现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,设弹簧的弹性势能与弹簧的形变量(即伸长量或缩短量)的平方成正比.小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动.已知小球A的质量也为m时,它们恰能回到O点(设3个小球直径相等,且远小于x0,略小于直圆筒内径),问小球A至少在B球正上方多少距离处自由落下,与B球粘连后一起运动,可带动小球C离开筒底.
质量为m的小球B与质量为2m的小球C之间用一根轻质弹簧连接,现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,设弹簧的弹性势能与弹簧的形变量(即伸长量或缩短量)的平方成正比.小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动.已知小球A的质量也为m时,它们恰能回到O点(设3个小球直径相等,且远小于x0,略小于直圆筒内径),问小球A至少在B球正上方多少距离处自由落下,与B球粘连后一起运动,可带动小球C离开筒底.分析:小球A下落过程只受重力,机械能守恒;由机械能守恒定律可求得小球A的末速度;再由动量守恒可求得碰后的共同速度;如果让B带动C向上运动,应使弹簧伸长到使弹力大于等于C的重力;由机械能守恒定律可列出表达式,联立以上关系可求得小球至少在B球上方的距离.
解答:解:设小球A由初始位置下落至小球B碰撞前的速度为v0,由机械能守恒得:
mg3x0=
mv02 (1)
所以:v0=
(2)
设小球A与小球B碰撞后共同速度为v1,由动量守恒得:mv0=2mv1 (3)
所以:v1=
(4)
设弹簧初始的弹性势能为EP,则碰撞后回到O点时机械能守恒得:
2mgx0=
×2mv12+EP (5)
由(1)(3)(5)式可得:EP=
mgx0 (6)
小球B处于平衡时,有(设k为弹簧的劲度系数)
kx0=mg (7)
当小球C刚好被拉离筒底时,有:
kx=2mg (8)
由(7)(8)可知:x=2x0 (9)
根据题中条件可知,小球C刚好被拉离筒底时,弹簧弹性势能为:E'P=4EP (10)
设小球A至少在B球正上方h处高处下落,且与小球B碰撞前速度为v3,由机械能守恒,得:
mgh=
mv32 (11)
设小球A与小球B碰撞后共同速度为v4
由动量守恒可得:mv3=2mv4 (12)
由机械能守恒得:
×2mv42+EP=E'p+2mg×3x0 (13)
由(6)(10)(11)(12)(13)可得:h=15x0 (14)
答:小球至少距B球15x0才能带动C离开筒底.
mg3x0=
| 1 |
| 2 |
所以:v0=
| 6gx0 |
设小球A与小球B碰撞后共同速度为v1,由动量守恒得:mv0=2mv1 (3)
所以:v1=
| 1 |
| 2 |
| 6gx0 |
设弹簧初始的弹性势能为EP,则碰撞后回到O点时机械能守恒得:
2mgx0=
| 1 |
| 2 |
由(1)(3)(5)式可得:EP=
| 1 |
| 2 |
小球B处于平衡时,有(设k为弹簧的劲度系数)
kx0=mg (7)
当小球C刚好被拉离筒底时,有:
kx=2mg (8)
由(7)(8)可知:x=2x0 (9)
根据题中条件可知,小球C刚好被拉离筒底时,弹簧弹性势能为:E'P=4EP (10)
设小球A至少在B球正上方h处高处下落,且与小球B碰撞前速度为v3,由机械能守恒,得:
mgh=
| 1 |
| 2 |
设小球A与小球B碰撞后共同速度为v4
由动量守恒可得:mv3=2mv4 (12)
由机械能守恒得:
| 1 |
| 2 |
由(6)(10)(11)(12)(13)可得:h=15x0 (14)
答:小球至少距B球15x0才能带动C离开筒底.
点评:本题考查动量守恒定律、牛顿运动定律及运动学公式,过程较为复杂,要求学生能正确理解运动过程,并能找出应用的物理规律进行列式计算.

练习册系列答案
相关题目
 (2013?南昌二模)如图所示,在光滑水平面上,质量为m的小球B连接着一个轻质弹簧,弹簧与小球 均处于静止状态.质量为2m的小球A以大小为v0的水平速度向右运动,接触弹簧后逐渐压缩弹簧并使B运动,经过一段时间,A与弹簧分离.
(2013?南昌二模)如图所示,在光滑水平面上,质量为m的小球B连接着一个轻质弹簧,弹簧与小球 均处于静止状态.质量为2m的小球A以大小为v0的水平速度向右运动,接触弹簧后逐渐压缩弹簧并使B运动,经过一段时间,A与弹簧分离. (2009?枣庄一模)如图所示,一轻绳绕过无摩擦的两轻质的小定滑轮O1、O2跟质量为m的小球B连接,另一端与套在光滑直杆上质量也为m的小物块A连接.已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°.直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L.设直杆足够长,小球运动过程中不会与其它物体相碰,重力加速度为g.现将小物块A从C点由静止释放.
(2009?枣庄一模)如图所示,一轻绳绕过无摩擦的两轻质的小定滑轮O1、O2跟质量为m的小球B连接,另一端与套在光滑直杆上质量也为m的小物块A连接.已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°.直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L.设直杆足够长,小球运动过程中不会与其它物体相碰,重力加速度为g.现将小物块A从C点由静止释放.
