题目内容
如图所示为某探究活动小组设计的节能运动系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为μ=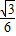 .木箱在轨道端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,当木箱下滑L距离时,轻弹簧被压缩至最短,此时自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.(g取10m/s2)
.木箱在轨道端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,当木箱下滑L距离时,轻弹簧被压缩至最短,此时自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.(g取10m/s2)求:(1)木箱不与弹簧接触时,木箱下滑的加速度与上滑的加速度;
(2)此过程中弹簧最大的弹性势能.
(3)
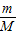 比值为多少.
比值为多少.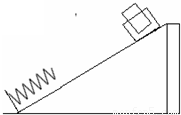
【答案】分析:(1)对下滑过程和上滑过程分别进行受力分析,根据牛顿第二定律求出下滑和上滑过程中的加速度.
(2)对上滑过程运用能量守恒定律,弹性势能转化为木箱的重力势能和摩擦产生的内能.
(3)在下滑过程中,木箱和货物的重力势能转化为弹簧的弹性势能以及摩擦产生的内能,根据上滑过程和下滑过程弹性势能相等,求出木箱和货物的质量比.
解答:解:(1)设下滑时加速度为a1,弹起离开弹簧后加速度为a2,则有
(M+m)gsin30°-μ(M+m)gcos30°=(M+m)a1
解得:a1=2.5m/s2
Mgsin30°+μMgcos30°=Ma2
解得:a2=7.5m/s2
故下滑和上滑的加速度分别为2.5m/s2和7.5m/s2.
(2)在木箱上滑的过程中,重力势能增加,动能变化为零,弹性势能减小,摩擦产生的内能增加.
根据能量守恒定律有:
弹簧最大的弹性势能为:W弹=M gLsin30°+μMgLcos30°
(3)在木箱与货物一起向下滑到卸货过程中,
则有(M+m)gLsin30°=μ(M+m)gLcos30°+W弹
卸下货后,木箱被弹回轨道顶端,有
W弹-M gLsin30°-μMgLcos30°=0
由以上解得: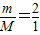
故货物和木箱的质量比为2:1.
点评:本题综合运用了牛顿第二定律以及能量守恒定律,也可以用动能定理求解,关键是合理地选择研究的过程.
(2)对上滑过程运用能量守恒定律,弹性势能转化为木箱的重力势能和摩擦产生的内能.
(3)在下滑过程中,木箱和货物的重力势能转化为弹簧的弹性势能以及摩擦产生的内能,根据上滑过程和下滑过程弹性势能相等,求出木箱和货物的质量比.
解答:解:(1)设下滑时加速度为a1,弹起离开弹簧后加速度为a2,则有
(M+m)gsin30°-μ(M+m)gcos30°=(M+m)a1
解得:a1=2.5m/s2
Mgsin30°+μMgcos30°=Ma2
解得:a2=7.5m/s2
故下滑和上滑的加速度分别为2.5m/s2和7.5m/s2.
(2)在木箱上滑的过程中,重力势能增加,动能变化为零,弹性势能减小,摩擦产生的内能增加.
根据能量守恒定律有:
弹簧最大的弹性势能为:W弹=M gLsin30°+μMgLcos30°
(3)在木箱与货物一起向下滑到卸货过程中,
则有(M+m)gLsin30°=μ(M+m)gLcos30°+W弹
卸下货后,木箱被弹回轨道顶端,有
W弹-M gLsin30°-μMgLcos30°=0
由以上解得:
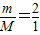
故货物和木箱的质量比为2:1.
点评:本题综合运用了牛顿第二定律以及能量守恒定律,也可以用动能定理求解,关键是合理地选择研究的过程.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图所示为某探究活动小组设计的节能运输系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为μ=
如图所示为某探究活动小组设计的节能运输系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为μ=
| ||
| 6 |
| A、木箱与弹簧接触时速度达到最大 |
| B、货物的质量m等于木箱质量M的2倍 |
| C、木箱不与弹簧接触时,上滑的加速度小于下滑的加速度 |
| D、在木箱与货物从顶端滑到最低点的过程中,减少的重力势能大于弹簧的弹性势能 |
如图所示为某探究活动小组设计的节能运动系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为 .木箱在轨道顶端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,与轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.下列选项正确的是
.木箱在轨道顶端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,与轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.下列选项正确的是
| A.m=M |
| B.m=2M |
| C.木箱不与弹簧接触时,上滑的加速度大于下滑的加速度 |
| D.在木箱与货物从顶端滑到最低点的过程中,减少的重力势能全部转化为弹簧的弹性势能 |
 如图所示为某探究活动小组设计的节能运输系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为
如图所示为某探究活动小组设计的节能运输系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为 如图所示为某探究活动小组设计的节能运动系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为μ=
如图所示为某探究活动小组设计的节能运动系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为μ= =
= .木箱在轨道端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,当木箱下滑L距离时,轻弹簧被压缩至最短,此时自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.(g取10m/s2)
.木箱在轨道端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,当木箱下滑L距离时,轻弹簧被压缩至最短,此时自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.(g取10m/s2)
 比值为多少.
比值为多少.