Question

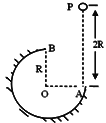
【题目】（多选）如图所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力。已知AP=2R，重力加速度为g，则小球从P到B的运动过程中（ ）。

A. 重力做功

B. 机械能减少

C. 合外力做功

D. 摩擦力做功

Answer 1

【答案】BC

【解析】A．根据重力做功的公式应有：WG=mg(2RR)=mgR，所以A错误；

B．小球到达B点时应满足：mg=①，

设阻力对小球做的功为Wf，从P到B过程由动能定理可得：mgR+Wf=0②，

联立①②解得：Wf=，即机械能减少，故B正确，D错误；

C:根据动能定理应有：W总=-0，代入可得：合外力做的功为：W总=，所以C正确；

故选：BC.