题目内容
(2011?黄冈模拟)如图甲所示,横截面为“ ”型、水平平行放置的金属导轨MN、PQ的NQ端固定着绝缘挡板,挡板中央栓接有轻质弹簧,弹簧自由端右侧的导轨光滑.放在导轨上的光滑金属滑块A质量M=0.60kg、电阻R=0.50Ω;绝缘滑块B质量m=0.4kg,与导轨之间的滑动摩擦因数μ=0.20.在导轨MP端加如图乙所示的脉冲电压U时,导轨之间产生磁场,滑块A即在安培力作用下做初速度为零的匀加速运动.在脉冲时间t0=0.50s内的任意时刻,A两端的电压u=U-e,e为A运动产生的感应电动势的大小.脉冲电压消失以后,滑块A撞击滑块B(撞击的时间极短).撞击后A、B-起向右运动,并压缩弹簧(弹簧始终在弹性限度内).已知从A、B碰撞到B与弹簧接触,历时t1=0.75s;B与A分离后继续运动t2=1.Os后静止.不计导轨的电阻、图示滑块的横向宽度和空气阻力,g取1Om/s2.求:
”型、水平平行放置的金属导轨MN、PQ的NQ端固定着绝缘挡板,挡板中央栓接有轻质弹簧,弹簧自由端右侧的导轨光滑.放在导轨上的光滑金属滑块A质量M=0.60kg、电阻R=0.50Ω;绝缘滑块B质量m=0.4kg,与导轨之间的滑动摩擦因数μ=0.20.在导轨MP端加如图乙所示的脉冲电压U时,导轨之间产生磁场,滑块A即在安培力作用下做初速度为零的匀加速运动.在脉冲时间t0=0.50s内的任意时刻,A两端的电压u=U-e,e为A运动产生的感应电动势的大小.脉冲电压消失以后,滑块A撞击滑块B(撞击的时间极短).撞击后A、B-起向右运动,并压缩弹簧(弹簧始终在弹性限度内).已知从A、B碰撞到B与弹簧接触,历时t1=0.75s;B与A分离后继续运动t2=1.Os后静止.不计导轨的电阻、图示滑块的横向宽度和空气阻力,g取1Om/s2.求:

(l)A、B分离时,B的速率;
(2)脉冲电压消失时,A的速率;
(3)脉冲电压U对时间t的变化率.
 ”型、水平平行放置的金属导轨MN、PQ的NQ端固定着绝缘挡板,挡板中央栓接有轻质弹簧,弹簧自由端右侧的导轨光滑.放在导轨上的光滑金属滑块A质量M=0.60kg、电阻R=0.50Ω;绝缘滑块B质量m=0.4kg,与导轨之间的滑动摩擦因数μ=0.20.在导轨MP端加如图乙所示的脉冲电压U时,导轨之间产生磁场,滑块A即在安培力作用下做初速度为零的匀加速运动.在脉冲时间t0=0.50s内的任意时刻,A两端的电压u=U-e,e为A运动产生的感应电动势的大小.脉冲电压消失以后,滑块A撞击滑块B(撞击的时间极短).撞击后A、B-起向右运动,并压缩弹簧(弹簧始终在弹性限度内).已知从A、B碰撞到B与弹簧接触,历时t1=0.75s;B与A分离后继续运动t2=1.Os后静止.不计导轨的电阻、图示滑块的横向宽度和空气阻力,g取1Om/s2.求:
”型、水平平行放置的金属导轨MN、PQ的NQ端固定着绝缘挡板,挡板中央栓接有轻质弹簧,弹簧自由端右侧的导轨光滑.放在导轨上的光滑金属滑块A质量M=0.60kg、电阻R=0.50Ω;绝缘滑块B质量m=0.4kg,与导轨之间的滑动摩擦因数μ=0.20.在导轨MP端加如图乙所示的脉冲电压U时,导轨之间产生磁场,滑块A即在安培力作用下做初速度为零的匀加速运动.在脉冲时间t0=0.50s内的任意时刻,A两端的电压u=U-e,e为A运动产生的感应电动势的大小.脉冲电压消失以后,滑块A撞击滑块B(撞击的时间极短).撞击后A、B-起向右运动,并压缩弹簧(弹簧始终在弹性限度内).已知从A、B碰撞到B与弹簧接触,历时t1=0.75s;B与A分离后继续运动t2=1.Os后静止.不计导轨的电阻、图示滑块的横向宽度和空气阻力,g取1Om/s2.求:
(l)A、B分离时,B的速率;
(2)脉冲电压消失时,A的速率;
(3)脉冲电压U对时间t的变化率.
分析:(1)A与B碰后,只受到B的摩擦力作用,受到发生变化,可以使用动量定理求出碰后A与B的速度,以及A、B分离时的速度;
(2)碰撞的时间短,可以使用动量守恒定律求出A、B碰撞前的速度;
(3)由运动学的公式求出A的加速度,再使用法拉第电磁感应定律和牛顿第二定律,写出电压U的表达式,最后求出U对时间的变化率.
(2)碰撞的时间短,可以使用动量守恒定律求出A、B碰撞前的速度;
(3)由运动学的公式求出A的加速度,再使用法拉第电磁感应定律和牛顿第二定律,写出电压U的表达式,最后求出U对时间的变化率.
解答:解:(1)当A、B分离时,A、B速度相等,设为v2.根据动量定理有:μmgt2=mv2
代入已知数据得B的速度:v2=2.0m/s
(2)设A、B碰撞时,A的速度为v0,碰后A、B共同速度为v1.A、B一起向右运动,与弹簧接触时速度即为v2.
从A、B碰后到与弹簧接触的过程,根据动量定理有:-μmgt1=(M+m)v2-(M+m)v1
代入已知数据得:v1=2.6m/s
A、B碰撞过程由动量守恒定律有:Mv0=(M+m)v1
代入已知数据得:v0=
m/s=4.33m/s
(3)由v0=a0t0知滑块A做匀加速运动加速度:a0=8.66m/s2
由法拉第电磁感应定律知:E=Bdv ①
由欧姆定律知t0=0.50s内滑块A中电流:i=
②
t0=0.50s内滑块A受到的安倍力:F=Bid ③
由牛顿第二定律有:F=Ma0 ④
由①②③④整理得:U=Bda0t+
⑤
将已知数据代入⑤可求得脉冲电压U对时间t的变化率为:
k=Bda0=
=11.3V/s
答:(l)A、B分离时,B的速率是2.0m/s;
(2)脉冲电压消失时,A的速率4.33m/s;
(3)脉冲电压U对时间t的变化率11.3V/s.
代入已知数据得B的速度:v2=2.0m/s
(2)设A、B碰撞时,A的速度为v0,碰后A、B共同速度为v1.A、B一起向右运动,与弹簧接触时速度即为v2.
从A、B碰后到与弹簧接触的过程,根据动量定理有:-μmgt1=(M+m)v2-(M+m)v1
代入已知数据得:v1=2.6m/s
A、B碰撞过程由动量守恒定律有:Mv0=(M+m)v1
代入已知数据得:v0=
| 13 |
| 3 |
(3)由v0=a0t0知滑块A做匀加速运动加速度:a0=8.66m/s2
由法拉第电磁感应定律知:E=Bdv ①
由欧姆定律知t0=0.50s内滑块A中电流:i=
| U-Bdv |
| R |
t0=0.50s内滑块A受到的安倍力:F=Bid ③
由牛顿第二定律有:F=Ma0 ④
由①②③④整理得:U=Bda0t+
| RMa0 |
| bD |
将已知数据代入⑤可求得脉冲电压U对时间t的变化率为:
k=Bda0=
| 169 |
| 15 |
答:(l)A、B分离时,B的速率是2.0m/s;
(2)脉冲电压消失时,A的速率4.33m/s;
(3)脉冲电压U对时间t的变化率11.3V/s.
点评:该题属于力电综合的题目,使用到的公式比较多,涉及的情景相对复杂,要求学生具备较强的综合能力.

练习册系列答案
相关题目
 (2011?黄冈模拟)如图所示,水平细线OA和倾斜细线OB将小球悬挂于0点,小球处于平衡状态.细线OB与竖直方向的夹角θ=60°,对小球的拉力为F1.烧断水平细线,当小球摆到最低点时,细线OB对小球的拉力为F2.不计细线的伸长及一切阻力,则F1与F2的大小之比等于( )
(2011?黄冈模拟)如图所示,水平细线OA和倾斜细线OB将小球悬挂于0点,小球处于平衡状态.细线OB与竖直方向的夹角θ=60°,对小球的拉力为F1.烧断水平细线,当小球摆到最低点时,细线OB对小球的拉力为F2.不计细线的伸长及一切阻力,则F1与F2的大小之比等于( ) (2011?黄冈模拟)图甲中,上面的广口瓶里是空气,下面的广口瓶里是二氧化氮气体,两瓶中间隔有玻璃板.图乙中,容器壁导热性能良好,光滑活塞的质量不可忽略,下面密闭着一定质量的理想气体.下列有关图甲、图乙的说法,其中正确的是( )
(2011?黄冈模拟)图甲中,上面的广口瓶里是空气,下面的广口瓶里是二氧化氮气体,两瓶中间隔有玻璃板.图乙中,容器壁导热性能良好,光滑活塞的质量不可忽略,下面密闭着一定质量的理想气体.下列有关图甲、图乙的说法,其中正确的是( )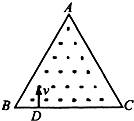 (2011?黄冈模拟)边长为2a的等边三角形ABC内分布着磁感应强度为B,方向垂直于纸面向外的匀强磁场.在BC边上的D点有一粒子源,不断地以不同的速率向磁场区域发射质量为m、电量为+q的粒子,所发射的粒子速度均垂直于BC边.若CD=
(2011?黄冈模拟)边长为2a的等边三角形ABC内分布着磁感应强度为B,方向垂直于纸面向外的匀强磁场.在BC边上的D点有一粒子源,不断地以不同的速率向磁场区域发射质量为m、电量为+q的粒子,所发射的粒子速度均垂直于BC边.若CD= (2011?黄冈模拟)如图甲所示,静止在水平面C上的长木板B左端放着小物块A.某时刻,A受到水平向右的外力F作用,F随时间t的变化规律如图乙所示.设A、B和B、C之间的滑动摩擦力大小分别为F1和F2,各物体之间的滑动摩擦力大小等于最大静摩擦力,且F1大于F2,则在A、B没有分离的过程中,下面可以定性地描述长木板B运动的v-t图象是( )
(2011?黄冈模拟)如图甲所示,静止在水平面C上的长木板B左端放着小物块A.某时刻,A受到水平向右的外力F作用,F随时间t的变化规律如图乙所示.设A、B和B、C之间的滑动摩擦力大小分别为F1和F2,各物体之间的滑动摩擦力大小等于最大静摩擦力,且F1大于F2,则在A、B没有分离的过程中,下面可以定性地描述长木板B运动的v-t图象是( )