题目内容
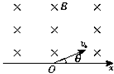如图所示，x轴上方有垂直纸面向里的匀强磁场．有两个质量相同，电荷量也相同的带正、负电的离子（不计重力），以相同速度从O点射入磁场中，射入方向与x轴均夹30°角．求正、负离子在磁场中运动半径比| r正 |
| r负 |
| t正 |
| t负 |
分析：离子射入磁场中，由于洛伦兹力作用而做匀速圆周运动，洛伦兹力充当向心力，由牛顿第二定律求得半径之比．由圆周运动的规律得到周期表达式，根据轨迹对应的圆心角，求时间之比．
解答：解：（1）由于离子所需向心力由洛伦兹力提供，则：
qvB=
①
故：r=
②
由于正负离子的速度、带电量是相同的，因此：
=
（2）如图所示，由洛伦兹力提供向心力得：qvB=m(
)2r ③
由②③式得：T=
由于正负离子的质量和带电量都相同，因此周期也相同．
而由图可知：轨迹圆心角分别为Φ正=2π-2θ=
，Φ负=2θ=
故：t正=
T，t负=
T
因此：
=
=
答：正、负离子在磁场中运动半径比
是
，时间比
是
．
qvB=
| mv2 |
| r |
故：r=
| mv |
| qB |
由于正负离子的速度、带电量是相同的，因此：
| r正 |
| r负 |
| 1 |
| 1 |
（2）如图所示，由洛伦兹力提供向心力得：qvB=m(
| 2π |
| T |
由②③式得：T=
| 2πm |
| qB |
由于正负离子的质量和带电量都相同，因此周期也相同．
而由图可知：轨迹圆心角分别为Φ正=2π-2θ=
| 5π |
| 3 |
| π |
| 3 |
故：t正=
| Φ 正 |
| 2π |
| Φ 负 |
| 2π |
因此：
| t正 |
| t负 |
| Φ正 |
| Φ负 |
| 5 |
| 1 |
答：正、负离子在磁场中运动半径比
| r正 |
| r负 |
| 1 |
| 1 |
| t正 |
| t负 |
| 5 |
| 1 |
点评：定圆心和半径、画轨迹是解题的基础．带电粒子垂直于磁场进入一匀强磁场后在洛伦兹力作用下必作匀速圆周运动，抓住运动中的任两点处的速度，分别作出各速度的垂线，则二垂线的交点必为圆心；或者用垂径定理及一处速度的垂线也可找出圆心；再利用数学知识求出圆周运动的半径及粒子经过的圆心角从而解答物理问题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
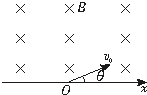如图所示，x轴上方有垂直纸面向里的匀强磁场．有两个质量相同，电荷量也相同的带正、负电的离子（不计重力），以相同速度从O点射入磁场中，射入方向与x轴均夹θ角．则正、负离子在磁场中（ ）?
如图所示，x轴上方有竖直向下的匀强电场，从x轴A点（
如图所示，x轴上方有垂直纸面向里的匀强磁场．有两个质量相同，电荷量也相同的带正、负电的离子（不计重力），以相同速度从O点射入磁场中，射入方向与x轴均夹θ角．则正、负离子在磁场中（ ）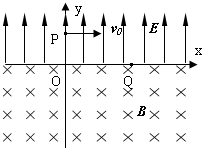
如图所示，x轴上方有一匀强电场，方向与y轴平行；x轴下方有一匀强磁场，方向垂直纸面向里．一质量为m、电量为-q（q＞0）的粒子以速度v0从y轴上的P点平行x轴方向射入电场后，从x轴上的Q点进入磁场，并从坐标原点O离开磁场．已知OP=L，OQ=2L．不计重力和一切摩擦，求：