Question

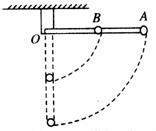
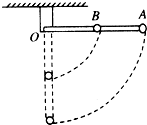长为L的杆（有一定的质量）可绕O在竖直平面内无摩擦转动，质量为M的小球A固定于杆端点，质量为m的小球B固定于杆中点，且M=2m，开始杆处于水平，由静止释放，当杆转到竖直位置时，下列说法正确的是（　　）

• A．A球对杆做负功
• B．A球的机械能增加
• C．A球的机械能减少
• D．A球在最低点速度大小为

  2

  3

  5gL

Answer 1

分析：对A、B两球组成的系统，在运动的过程中只有重力做功，系统机械能守恒，抓住A、B的角速度相等，根据A、B的速度关系，利用系统机械能守恒定律求出A、B两球的速度，再根据动能定理分别求出轻杆对A、B两球分别做的功．

解答：解：若取A的最低点为零重力势能参考平面，根据系统机械能守恒得：
MgL=

1

2

M

v

2 A

+

1

2

m

v

2 B

+

1

2

mgL
又因A球对B球在各个时刻对应的角速度相同，故v_A=2v_B
联立两式得：v_A=2

gL 3

    v_B=

gL 3

根据动能定理，可解出杆对A、B做的功．
对于A有：W_A+MgL=

1

2

MvA2-0
即：W_A=-

1

3

MgL，
综上，故AB正确，CD错误
故选：AB

点评：解决本题的关键知道A、B两球在运动的过程中，系统机械能守恒，因为杆子做功为变力做功，只能求出A、B的速度，根据动能定理求出杆子的做功．