题目内容
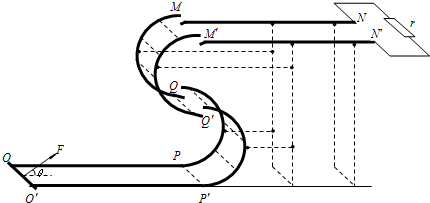
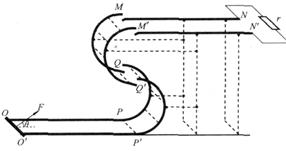
如图所示,固定在上、下两层水平面上的平行金属导轨MN、M′N′和OP、O′P′间距都是l,二者之间固定有两组竖直半圆形轨道PQM和P′Q′M′,它们是用绝缘材料制成的,两轨道间距也均为l,且PQM和P′Q′M′的竖直高度均为4R,两组半圆形轨道的半径均为R.轨道的QQ′端、MM′端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架.下层金属导轨接有电源,当将一金属杆沿垂直导轨方向搭接在两导轨上时,将有电流从电源正极流出,经过导轨和金属杆流回电源负极.此时金属杆将受到导轨中电流所形成磁场的安培力作用而运动.运动过程中金属杆始终与导轨垂直,且接触良好.当金属杆由静止开始向右运动4R到达水平导轨末端PP′位置时其速度大小vP=4
.已知金属杆质量为m,两轨道间的磁场可视为匀强磁场,其磁感应强度与电流的关系为B=kI(k为已知常量),金属杆在下层导轨的运动可视为匀加速运动,运动中金属杆所受的摩擦阻力、金属杆和导轨的电阻均可忽略不计.

(1)求金属杆在下层导轨运动过程中通过它的电流大小;
(2)金属杆由PP′位置无碰撞地水平进入第一组半圆轨道PQ和P′Q′,又在狭缝Q和Q′无碰撞地水平进入第二组半圆形轨道QM和Q′M′的内侧.求金属杆由PP′处到MM′处过程中动量的增量;
(3)金属杆由第二个半圆轨道的最高位置MM′处,以一定的速度在M和M′处沿对接狭缝无碰撞地水平进入上层金属导轨后,能沿着上层金属导轨滑行.设上层水平导轨足够长,其右端连接的定值电阻阻值为r,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中(不计此时导轨中电流产生的磁场的影响).求金属杆在上层水平金属导轨上能滑行过程中通过导体横截面的电荷量.
| gR |

(1)求金属杆在下层导轨运动过程中通过它的电流大小;
(2)金属杆由PP′位置无碰撞地水平进入第一组半圆轨道PQ和P′Q′,又在狭缝Q和Q′无碰撞地水平进入第二组半圆形轨道QM和Q′M′的内侧.求金属杆由PP′处到MM′处过程中动量的增量;
(3)金属杆由第二个半圆轨道的最高位置MM′处,以一定的速度在M和M′处沿对接狭缝无碰撞地水平进入上层金属导轨后,能沿着上层金属导轨滑行.设上层水平导轨足够长,其右端连接的定值电阻阻值为r,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中(不计此时导轨中电流产生的磁场的影响).求金属杆在上层水平金属导轨上能滑行过程中通过导体横截面的电荷量.
分析:(1)根据匀变速直线运动的速度位移公式求出匀加速直线运动的加速度,结合牛顿第二定律求出电流的大小.
(2)根据动能定理求出金属杆到达MM′的速度,从而得出动量的增加量.
(3)根据动量定理求出金属杆在上层水平金属导轨上能滑行过程中通过导体横截面的电荷量.
(2)根据动能定理求出金属杆到达MM′的速度,从而得出动量的增加量.
(3)根据动量定理求出金属杆在上层水平金属导轨上能滑行过程中通过导体横截面的电荷量.
解答:解:(1)金属杆在下层导轨运动的加速度a=
=2g
根据牛顿第二定律得,BIl=kI2l=ma
联立两式解得I=
.
(2)根据动能定理得,-?mg4R=
mv2-
mvp2
解得v=2
.
则动量的增量△P=m(2
-4
).
(3)根据动量定理得,BIL?△t=mv
则Blq=mv
解得q=
=
.
答:(1)金属杆在下层导轨运动过程中通过它的电流大小为
;
(2)金属杆由PP′处到MM′处过程中动量的增量为△P=m(2
-4
);
(3)金属杆在上层水平金属导轨上能滑行过程中通过导体横截面的电荷量为
.
| vp2 |
| 2?4R |
根据牛顿第二定律得,BIl=kI2l=ma
联立两式解得I=
|
(2)根据动能定理得,-?mg4R=
| 1 |
| 2 |
| 1 |
| 2 |
解得v=2
| 2gR |
则动量的增量△P=m(2
| 2gR |
| gR |
(3)根据动量定理得,BIL?△t=mv
则Blq=mv
解得q=
| mv |
| Bl |
2m
| ||
| Bl |
答:(1)金属杆在下层导轨运动过程中通过它的电流大小为
|
(2)金属杆由PP′处到MM′处过程中动量的增量为△P=m(2
| 2gR |
| gR |
(3)金属杆在上层水平金属导轨上能滑行过程中通过导体横截面的电荷量为
2m
| ||
| Bl |
点评:本题考查了牛顿第二定律、动量定理、动能定理的综合运用,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 、
、 和
和 、
、 间距都是
间距都是 ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道 和
和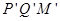 ,两轨道间距也均为
,两轨道间距也均为 端、
端、 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端 位置,金属杆在与水平成
位置,金属杆在与水平成 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端 位置时其速度大小
位置时其速度大小 。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。 ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小; 和
和 ,又在对接狭缝
,又在对接狭缝 和
和 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道 和
和 的内
的内 ,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置