题目内容
 如图,半径R=0.4m光滑半圆环轨道处在竖直平面内,半圆环与粗糙在水平地面相切于圆环的端点A.一质量m=0.1Kg的小球以初速v0=7m/s在水平地面上向左做加速度a=3m/s2的匀减速直线运动,运动x=4m后,冲竖直半圆环,最后小球落在C点.(取g=10m/s2).求
如图,半径R=0.4m光滑半圆环轨道处在竖直平面内,半圆环与粗糙在水平地面相切于圆环的端点A.一质量m=0.1Kg的小球以初速v0=7m/s在水平地面上向左做加速度a=3m/s2的匀减速直线运动,运动x=4m后,冲竖直半圆环,最后小球落在C点.(取g=10m/s2).求(1)小球运动到A处时的速度.
(2)小球能否到达轨道最高点B,不能请说明理由,若能则求出在B点时小球的速度.
(3)求AC间的距离.
分析:(1)小球从静止运动到A的过程是匀减速直线运动,根据位移速度公式即可求得;
(2)小球沿半圆环轨道做圆周运动,要达到最高点有个最小速度,可根据圆周运动的公式算出最小速度,再根据动能定理算出B的速度,如果B的速度大于最小速度就能达到;
(3)小球从B点抛出做平抛运动,根据平抛运动的规律即可求得.
(2)小球沿半圆环轨道做圆周运动,要达到最高点有个最小速度,可根据圆周运动的公式算出最小速度,再根据动能定理算出B的速度,如果B的速度大于最小速度就能达到;
(3)小球从B点抛出做平抛运动,根据平抛运动的规律即可求得.
解答:解:(1)小球在水平地面向左匀减速运动4m的过程中,有:
vA2-v02=2as
解得:vA=5m/s
(2)假设小球能够通过最高点B,从A到B的过程运用动能定理得:
mvB2 -
mvA2=2mgR
解得:vB=3m/s
小球恰好能到最高点B应满足:mg=m
解得:vm=2m/s
因为vB>vm
所以能通过最高点B.
(3)小球从B点抛出后做平抛运动,有2R=
gt2
解得:t=0.4s
xAC=vBt=1.2m
答:(1)小球运动到A处时的速度为5m/s;(2)小球能到达轨道最高点B,B点的速度为3m/s;(3)AC间的距离为1.2m.
vA2-v02=2as
解得:vA=5m/s
(2)假设小球能够通过最高点B,从A到B的过程运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:vB=3m/s
小球恰好能到最高点B应满足:mg=m
| vm2 |
| R |
解得:vm=2m/s
因为vB>vm
所以能通过最高点B.
(3)小球从B点抛出后做平抛运动,有2R=
| 1 |
| 2 |
解得:t=0.4s
xAC=vBt=1.2m
答:(1)小球运动到A处时的速度为5m/s;(2)小球能到达轨道最高点B,B点的速度为3m/s;(3)AC间的距离为1.2m.
点评:该题是圆周运动和匀减速运动相结合的典型题型,注意判断能否达到最高点的判断方法,该题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
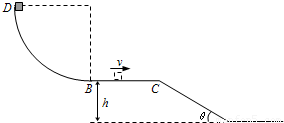
 如图,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=30°的光滑斜面连接,质量m=1kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数?=0.1,取g=10m/s2.求:
如图,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=30°的光滑斜面连接,质量m=1kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数?=0.1,取g=10m/s2.求: 如图所示,传送带的两个轮子半径均为r=0.2m,两个轮子最高点A、B在同一水平面 内,A、B间距离L=5m,半径R=0.4的固定、竖直光滑圆轨道与传送带相切于B点,C 点是圆轨道的最高点.质量m=0.1kg的小滑块与传送带之间的动摩擦因数μ=0.4.重力加速 度 g=10m/s2.求:
如图所示,传送带的两个轮子半径均为r=0.2m,两个轮子最高点A、B在同一水平面 内,A、B间距离L=5m,半径R=0.4的固定、竖直光滑圆轨道与传送带相切于B点,C 点是圆轨道的最高点.质量m=0.1kg的小滑块与传送带之间的动摩擦因数μ=0.4.重力加速 度 g=10m/s2.求: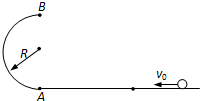 如图,半径R=0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A 且μ=0.4.一质量m=0.1kg的小球,以初速度v0=8m/s在粗糙水平地面上向左作直线运动,运动4m后,冲上竖直半圆环,经过最高点B后飞出.取重力加速度g=10m/s2.求:
如图,半径R=0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A 且μ=0.4.一质量m=0.1kg的小球,以初速度v0=8m/s在粗糙水平地面上向左作直线运动,运动4m后,冲上竖直半圆环,经过最高点B后飞出.取重力加速度g=10m/s2.求: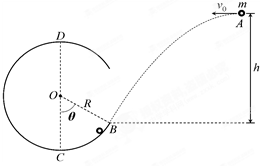 如图一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g=10m/s2.求:
如图一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g=10m/s2.求: