题目内容
13. 如图所示,在一水平向左的匀强电场中,光滑绝缘直角三角形斜劈ABC被固定在水平面上,其斜面长L=1.5m,倾角为θ=37°.有一个电荷量为q=3×10-5C、质量为m=4×10-3kg的带电小物块(可视为质点)恰能静止在斜面的顶端A处.g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,在一水平向左的匀强电场中,光滑绝缘直角三角形斜劈ABC被固定在水平面上,其斜面长L=1.5m,倾角为θ=37°.有一个电荷量为q=3×10-5C、质量为m=4×10-3kg的带电小物块(可视为质点)恰能静止在斜面的顶端A处.g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)AB两点间的电势差UAB;
(2)若电场强度减小为原来的一半时小物块从A下滑到B的时间t.
分析 (1)对小球受力分析,有共点力平衡求的电场强度,由U=Ed求的电势差;
(2)
解答 解:(1)对小物块静止在斜面的顶端A处时受力情况如图所示,由物体平衡条件有:
Nsinθ-qE=0…①
Ncosθ-mg=0…②
UAB=ELcosθ…③
联解①②③并代入数据得:
UAB=1200V…④
(2)若电场强度减小为原来的$\frac{1}{2}$,则有牛顿运动定律有:
$mgsinθ-q•\frac{E}{2}cosθ=ma$…⑤
$L=\frac{1}{2}a{t}^{2}$…⑥
联解⑤⑥并代入数据得:
t=1s
答:(1)AB两点间的电势差UAB为1200V
(2)若电场强度减小为原来的一半时小物块从A下滑到B的时间t为1s.
点评 本题主要考查了电场力作用下的共点力平衡和牛顿第二定律,加速度是关键

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
3. 在第16届广州亚运会体操男子单杠决赛中,中国选手张成龙以16.225分的成绩获得冠军.如图所示,他双手握住单杠,双臂平行使身体悬空,当他两手之间的距离增大、身体悬空并处于静止时,单杠对手臂的力T及它们的合力F的大小变化情况为( )
在第16届广州亚运会体操男子单杠决赛中,中国选手张成龙以16.225分的成绩获得冠军.如图所示,他双手握住单杠,双臂平行使身体悬空,当他两手之间的距离增大、身体悬空并处于静止时,单杠对手臂的力T及它们的合力F的大小变化情况为( )
 在第16届广州亚运会体操男子单杠决赛中,中国选手张成龙以16.225分的成绩获得冠军.如图所示,他双手握住单杠,双臂平行使身体悬空,当他两手之间的距离增大、身体悬空并处于静止时,单杠对手臂的力T及它们的合力F的大小变化情况为( )
在第16届广州亚运会体操男子单杠决赛中,中国选手张成龙以16.225分的成绩获得冠军.如图所示,他双手握住单杠,双臂平行使身体悬空,当他两手之间的距离增大、身体悬空并处于静止时,单杠对手臂的力T及它们的合力F的大小变化情况为( )| A. | T增大,F增大 | B. | T增大,F不变 | C. | T增大,F减小 | D. | T减小,F不变 |
8. 如图所示,电源电动势为E,内阻为r,滑动变阻器电阻为R,两平行金属极板a、b间有垂直纸面向里的匀强磁场,一束速度为v的带正电粒子正好匀速穿过两板.闭合开关,不计带电粒子的重力.以下说法正确的是( )
如图所示,电源电动势为E,内阻为r,滑动变阻器电阻为R,两平行金属极板a、b间有垂直纸面向里的匀强磁场,一束速度为v的带正电粒子正好匀速穿过两板.闭合开关,不计带电粒子的重力.以下说法正确的是( )
 如图所示,电源电动势为E,内阻为r,滑动变阻器电阻为R,两平行金属极板a、b间有垂直纸面向里的匀强磁场,一束速度为v的带正电粒子正好匀速穿过两板.闭合开关,不计带电粒子的重力.以下说法正确的是( )
如图所示,电源电动势为E,内阻为r,滑动变阻器电阻为R,两平行金属极板a、b间有垂直纸面向里的匀强磁场,一束速度为v的带正电粒子正好匀速穿过两板.闭合开关,不计带电粒子的重力.以下说法正确的是( )| A. | 将滑片P上滑一点,粒子将可能从下极板边缘射出 | |
| B. | 将a极板下移一点,粒子将继续沿直线穿出 | |
| C. | 将滑片P下滑一点,粒子将可能从下极板边缘射出 | |
| D. | 如果将开关断开,粒子将继续沿直线穿出 |
18. 如图所示,内壁光滑的半球形容器静止在粗糙水平面上.将一劲度系数为k的轻弹簧一端固定在半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、OP与水平方向的夹角为θ=30°.下列说法正确的是( )
如图所示,内壁光滑的半球形容器静止在粗糙水平面上.将一劲度系数为k的轻弹簧一端固定在半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、OP与水平方向的夹角为θ=30°.下列说法正确的是( )
 如图所示,内壁光滑的半球形容器静止在粗糙水平面上.将一劲度系数为k的轻弹簧一端固定在半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、OP与水平方向的夹角为θ=30°.下列说法正确的是( )
如图所示,内壁光滑的半球形容器静止在粗糙水平面上.将一劲度系数为k的轻弹簧一端固定在半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、OP与水平方向的夹角为θ=30°.下列说法正确的是( )| A. | 轻弹簧对小球的作用力大小为$\frac{\sqrt{3}}{2}$mg | |
| B. | 半球形容器相对于水平面有向左的运动趋势 | |
| C. | 半球形容器对小球的弹力和弹簧对小球的作用力的合力竖直向上 | |
| D. | 弹簧原长为R+$\frac{mg}{k}$ |
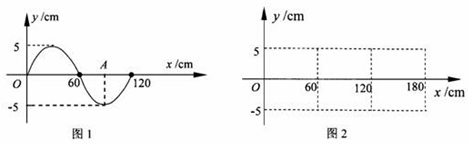
5.如图(1)所示,理想变压器原、副线圈的匝数比为20:1,R1=10Ω,R2=20Ω,C=100μF已知电阻R1两端的正弦交流电压如图(2)所示,则( )


| A. | 原线圈输入电压的最大值为 400V | B. | 交流电的频率为 100Hz | ||
| C. | 电容器C所带电量恒为2×10-3C | D. | 电阻R1消耗的电功率为 20W |