题目内容
如图所示，长为l的绝缘轻杆可绕杆固定轴O在竖直面内无摩擦转动，小球A电量为-q、小球B电量为+q，两球分别固定于杆的两端，AO=2BO，开始两球保持静止，杆与竖直方向夹角为θ．当加一场强为E且竖直向下的匀强电场后杆转动，转动过程中杆受的最大力矩是 ，B球获得的最大动能是 ．
【答案】分析：因力的大小方向不变，则其力矩的值确定于力臂的大小．再由轻杆的运动确定其位置范围求最大力矩．
在竖直位置动能最大．可求之．
解答：解：由整体的受的力矩可知轻杆在竖直线两侧摆动．则在图示位置力矩最大．
AB所受的电场力矩为同向，则总力矩为：
在达到竖直线是运动运动最大，因无电场时能处于平衡，则在转动过程中重力势能不发生变化．
二者的动能的增加量值为电势能的减少量．且B的重力臂等于A的重力臂的二分之一，则其质量为A的2倍．
则B的运动动能为A的
，为二者运动动能和的
．
A 的电势能的减小量为：
B 的电势能的减小量为：
则总电势能的减小量为：
+
=Eql（1-cosθ）
则B的运动动能为：
故答案为：Eqlsinθ，
Eql（1-cosθ）
点评：考查在力矩作用下物体的转动，明确能量的转化关系，难题．
在竖直位置动能最大．可求之．
解答：解：由整体的受的力矩可知轻杆在竖直线两侧摆动．则在图示位置力矩最大．
AB所受的电场力矩为同向，则总力矩为：
在达到竖直线是运动运动最大，因无电场时能处于平衡，则在转动过程中重力势能不发生变化．
二者的动能的增加量值为电势能的减少量．且B的重力臂等于A的重力臂的二分之一，则其质量为A的2倍．
则B的运动动能为A的
，为二者运动动能和的．A 的电势能的减小量为：
B 的电势能的减小量为：
则总电势能的减小量为：
+=Eql（1-cosθ）则B的运动动能为：
故答案为：Eqlsinθ，
Eql（1-cosθ）点评：考查在力矩作用下物体的转动，明确能量的转化关系，难题．
练习册系列答案
相关题目
如图所示，在场强为E的水平匀强电场中，一根长为l的绝缘杆，两端分别固定着带有电量+q和-q的小球（大小不计）．现让缘绝杆绕中点O逆时针转动α角，则转动中带电小球克服电场力做功为
如图所示，圆柱形绝热气缸（设其足够长）固定于水平面上，缸内用绝热活塞密封一定质量的理想气体，已知活塞与气缸壁的接触是光滑的，活塞的横截面积为S，大气压强为P0，电源和电热丝构成回路．可以对气体缓慢加热．开始时，电路未接通，系统处于平衡状态，封闭气体的温度为T1．现用两种方法使气缸内气体温度，均由T1缓慢升高到T2．第一次先将活塞固定，接通电路后电热丝产生的热量为Q1；第二次活塞不固定．可以缓慢自由移动，接通电路后电热丝产生的热量为Q2．
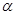角，则转动中带电小球克服电场力做功为___________．