题目内容
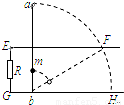
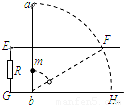
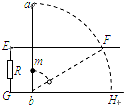如图所示，平行的光滑金属导轨EF和GH相距L，处于同一竖直平面内，EG间接有阻值为R的电阻，轻质金属杆ab长为2L，紧贴导轨竖直放置．在离b端L/2处固定套有一质量为m的小球．整个装置处于与导轨平面垂直、磁感应强度为 B的匀强磁场中，当ab杆由静止开始紧贴导轨绕b端向右倒下至水平位置时，球的速度为v．若导轨足够长，导轨及金属杆电阻不计，在此过程中通过电阻R的电量为分析：根据感应电荷量公式q=
求解通过电阻R的电量，其中△Φ是磁通量的变化量；对于球：从金属杆离开导轨EF到至水平位置的过程中，机械能守恒，即可求出金属杆离开导轨EF前小球的速度，由法拉第电磁感应定律求出感应电动势，由欧姆定律求解通过R的电流强度．
| △Φ |
| R |
解答：解：（1）通过电阻R的电量为q=
=
=
=
（2）设金属杆离开导轨EF前瞬间小球的速度为V，由几何知识得：∠FbH=30°．
从金属杆离开导轨EF到至水平位置的过程中，小球的机械能守恒，则有
mg
sin30°=
mv2-
mV2，得V=
由v=ωr，a端与球转动的角速度相等，则金属杆离开导轨EF前的一瞬间，a端的速度为Va=4V，杆将产生的感应电动势为E=B?2L
通过R的电流强度为I=
联立以上各式得：I=
故答案为：
；
| △Φ |
| R |
| B?△S |
| R |
B(
| ||||
| R |
| ||
| 2R |
（2）设金属杆离开导轨EF前瞬间小球的速度为V，由几何知识得：∠FbH=30°．
从金属杆离开导轨EF到至水平位置的过程中，小球的机械能守恒，则有
mg
| L |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
v2-
|
由v=ωr，a端与球转动的角速度相等，则金属杆离开导轨EF前的一瞬间，a端的速度为Va=4V，杆将产生的感应电动势为E=B?2L
| Va |
| 2 |
通过R的电流强度为I=
| E |
| R |
联立以上各式得：I=
| 2BL |
| R |
| 4v2-2gL |
故答案为：
| ||
| 2R |
| 2BL |
| R |
| 4v2-2gL |
点评：电磁感应问题中，感应电荷量表达式q=
是常用的经验公式．对于转动切割磁感线的类型，感应电动势公式E=BLv，v是杆中点的线速度大小．
| △Φ |
| R |
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图所示两平行的光滑金属导轨，相距为L，位于同一竖直平面内，两导轨间接有电阻R，轻质金属杆ab长为2L，紧贴导轨竖直放置，离b端为L/2处固定有质量为m的球．整个装置处于磁感应强度为B并垂直于导轨平面的匀强磁场中，当ab杆由静止开始紧贴导轨绕b端向右自由倒下至水平位置时，球的速度为v，若导轨足够长，导轨及金属杆电阻不计，试求此过程中：
”型装置,总质量为m,置于导轨上.导体棒中通以大小恒为I的电流(由外接恒流源产生,图中未画出).线框的边长为d(d＜l),电阻为R,下边与磁场区域上边界重合.将装置由静止释放,导体棒恰好运动到磁场区域下边界处返回,导体棒在整个运动过程中始终与导轨垂直.重力加速度为g.求:
