题目内容
 如图所示,一水平放置的光滑平行导轨上放一质量为m的金属杆,导轨间距为L,导轨的一端连接一阻值为R的电阻,金属杆与导轨的电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面.现给金属杆一个水平向右的初速度v0,让其自由滑行,导轨足够长,则金属杆滑行过程所受安培力F、运动速度v、加速度a、位移x大致图象正确的是( )
如图所示,一水平放置的光滑平行导轨上放一质量为m的金属杆,导轨间距为L,导轨的一端连接一阻值为R的电阻,金属杆与导轨的电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面.现给金属杆一个水平向右的初速度v0,让其自由滑行,导轨足够长,则金属杆滑行过程所受安培力F、运动速度v、加速度a、位移x大致图象正确的是( )A、 | B、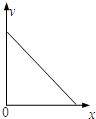 | C、 | D、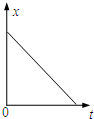 |
分析:导体棒受重力、支持力和向后的安培力,根据切割公式E=BLv、闭合电路欧姆定律、安培力公式F=BIL连列求解出安培力表达式进行分析.
解答:解:A、C、导体棒受重力、支持力和向后的安培力;
感应电动势为:E=BLv
感应电流为:I=
安培力为:F=BIL
联立得到:F=
∝v
根据牛顿第二定律,有:F=ma
故:
=ma
故a∝v
由于导体棒减速,故加速度也减小,即物体做加速度减小的减速运动,故v与t不成正比,故加速度a与力F均不与t成正比;
故A错误,C错误;
D、导体棒不是匀速运动,故x-t图象不是直线,故D错误;
B、安培力:F=
=ma=m
故:
v?△t=m?△v
求和,有:
∑v?△t=m?∑△v
故:
x=m(v0-v)
故v与x是线性关系;故B正确;
故选:B.
感应电动势为:E=BLv
感应电流为:I=
| E |
| R |
安培力为:F=BIL
联立得到:F=
| B2L2v |
| R |
根据牛顿第二定律,有:F=ma
故:
| B2L2v |
| R |
故a∝v
由于导体棒减速,故加速度也减小,即物体做加速度减小的减速运动,故v与t不成正比,故加速度a与力F均不与t成正比;
故A错误,C错误;
D、导体棒不是匀速运动,故x-t图象不是直线,故D错误;
B、安培力:F=
| B2L2v |
| R |
| △v |
| △t |
故:
| B2L2 |
| R |
求和,有:
| B2L2 |
| R |
故:
| B2L2 |
| R |
故v与x是线性关系;故B正确;
故选:B.
点评:本题关键是推导出安培力的表达式进行分析,明确导体棒做加速度不断减小的减速运动,难点在B选项,要结合微元法进行分析.

练习册系列答案
相关题目
 如图所示,一水平放置的平行板电容器,上下极板间存在匀强电场,其间有一带电小球从A点以某一初速度沿虚线AB运动,则在小球从A运动到B的过程中( )
如图所示,一水平放置的平行板电容器,上下极板间存在匀强电场,其间有一带电小球从A点以某一初速度沿虚线AB运动,则在小球从A运动到B的过程中( ) 如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( )
如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( ) 如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( )
如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( )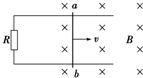 如图所示,一水平放置的平行导体框架宽度L=0.50m,接有电阻R=0.20Ω,磁感应强度B=0.40T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体棒ab电阻不计,当ab以v=4.0m/s的速度向右匀速滑动时.试求:
如图所示,一水平放置的平行导体框架宽度L=0.50m,接有电阻R=0.20Ω,磁感应强度B=0.40T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体棒ab电阻不计,当ab以v=4.0m/s的速度向右匀速滑动时.试求: