题目内容
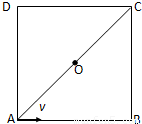
如图所示,在光滑绝缘的水平面内,对角线AC将边长为L的正方形分成ABC和ADC两个区域,ABC区域有垂直于水平面的匀强磁场,ADC区域有平行于DC并由C指向D的匀强电场.质量为m、带电量为+q的粒子从A点沿AB方向以v的速度射入磁场区域,从对角线AC的中点O进入电场区域.(1)判断磁场的方向并求出磁感应强度B的大小.
(2)讨论电场强度E在不同取值时,带电粒子在电场中运动的时间t.
【答案】分析:(1)根据左手定则,可以判断磁场方向垂直纸面向里.设带电粒子在磁场中运动的半径为r,根据向心力公式即可求解;
(2)根据平抛运动的基本公式求解电场强度,分情况进行讨论即可求解.
解答:解:(1)根据左手定则,可以判断磁场方向垂直纸面向里.
设带电粒子在磁场中运动的半径为r,有:Bqv=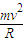 …①
…①
依题意,r=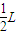 …②
…②
联立,解得: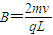 …③
…③
(2)设带电粒子恰好从D点离开电场时对应的电场强度为E,则有:
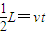 …④
…④
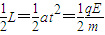 t2…⑤
t2…⑤
得: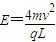 …⑥
…⑥
讨论:(i)当E≤E时,粒子从DC边离开电场,此时粒子在电场中运动的时间为t1
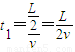 …⑦
…⑦
(ii)当E>E时,粒子从AD边离开电场,此时粒子在电场中运动的时间为t2,有:
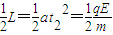
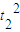
得: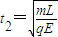
答:(1)磁场的方向垂直纸面向里,磁感应强度B的大小为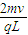 .
.
(2)当E≤E时,时间为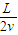 ,当E>E时,时间为
,当E>E时,时间为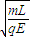 .
.
点评:本题是带电粒子在组合场中运动的问题,关键是分析粒子的受力情况和运动情况,用力学的方法处理.
(2)根据平抛运动的基本公式求解电场强度,分情况进行讨论即可求解.
解答:解:(1)根据左手定则,可以判断磁场方向垂直纸面向里.
设带电粒子在磁场中运动的半径为r,有:Bqv=
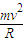 …①
…①依题意,r=
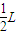 …②
…②联立,解得:
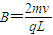 …③
…③(2)设带电粒子恰好从D点离开电场时对应的电场强度为E,则有:
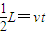 …④
…④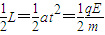 t2…⑤
t2…⑤得:
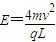 …⑥
…⑥讨论:(i)当E≤E时,粒子从DC边离开电场,此时粒子在电场中运动的时间为t1
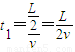 …⑦
…⑦(ii)当E>E时,粒子从AD边离开电场,此时粒子在电场中运动的时间为t2,有:
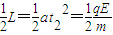
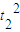
得:
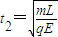
答:(1)磁场的方向垂直纸面向里,磁感应强度B的大小为
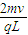 .
.(2)当E≤E时,时间为
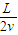 ,当E>E时,时间为
,当E>E时,时间为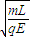 .
.点评:本题是带电粒子在组合场中运动的问题,关键是分析粒子的受力情况和运动情况,用力学的方法处理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
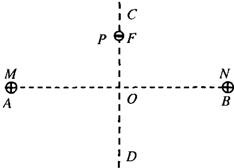 如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )
如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )| A、小球P的带电量缓慢减小,则它往复运动过程中振幅不断减小 | B、小球P的带电量缓慢减小,则它往复运动过程中每次经过O点时的速率不断减小 | C、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中周期不断减小 | D、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中振幅不断减小 |
 如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( )
如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( ) (2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为
(2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为 如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,
如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中, 如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求:
如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求: