Question

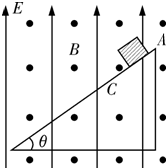如图所示，在相互垂直的匀强磁场和匀强电场中，有一倾角为θ的足够长的光滑绝缘斜面，磁感应强度为B，方向水平向外，电场强度为E，方向竖直向上．有一质量为m、带电量为+q的小滑块静止在斜面顶端，对斜面的正压力恰好为零．
（1）如果迅速把电场方向转为竖直向下，求小滑块能在斜面上连续滑行的最远距离L及所用时间t．
（2）如果在距A端 L/4远处的C点放一个相同质量但不带电的小物体，当滑块从A点由静止下滑到C点时两物体相碰并粘合在一起，则此粘合体在斜面上还能滑行多少时间和距离？

Answer 1

分析：（1）当电场竖直向上时，小球对斜面无压力，可知电场力和重力大小相等；当电场竖直向下时，小球受到向下的力为2mg；当小球恰好离开斜面时，在垂直于斜面的方向上合力为零，由此可求出此时的速度；在此过程中，电势能和重力势能转化为动能，由动能定理即可求出小球下滑的距离．
（2）滑块与物体碰撞过程，动量守恒，由动量守恒定律求出碰撞后的共同速度．当粘合体将要离开斜面时，斜面的支持力为零，在垂直于斜面的方向上合力为零，由此可求出此时的速度；
根据动能定理求出此粘合体在斜面上还能滑行的距离，由动量定理求出滑行的时间．

解答：解：（1）只有一个滑块运动时：
电场方向竖直向上时有  Eq=mg          
场强大小不变，转变为竖直向下时，滑块沿斜面连续下滑的最大距离L可根据动能定理有：
（mg+qE）Lsinθ=

1

2

mv ²                                     
即：2mgLsinθ=

1

2

mv ²
当滑块刚刚离开斜面时有：
Bqv=（mg+Eq）cosθ                                               
联立①②两式解得：L=

m2gcos2θ

B2q2sinθ

                           
再根据动量定理可知：t=

mv

2mgsinθ

=

m

Bqtanθ

                       
（2）两个物体先后运动：
设在C点处碰撞前滑块的速度为v，则有：2mg×

l

4

sinθ=

1

2

mv²             
设碰撞后粘合体速度为u，由动量守恒有：mv=2mu                     
当粘合体将要离开斜面时有：Bv′q=（2mg+Eq）cosθ=3mgcosθ           
根据动能定理，碰后两物体共同下滑的过程有：
3mgsinθ?S=

1

2

（2m） v′²-

1

2

（2m）u²                                
由上述各式可得粘合体在斜面上还能滑行的距离：
S=3

m2gcos2θ

B2q2sinθ

-

L

12

                                           
将L的结果代入后整理有：S=

35m2gcos2θ

12B2q2sinθ

粘合体在斜面上还能滑行的时间可由动量定理求得：t′=

2mv′-2mu

3mgsinθ

=

2m

Bqtanθ

-

gLsinθ

3gLsinθ

和
将L的结果代入后整理有：t′=

5

3

t=

5m

3Bqtanθ

答：
（1）滑块能在斜面上连续滑行的最远距离L为

m2gcos2θ

B2q2sinθ

，所用时间t为

m

Bqtanθ

．
（2）此粘合体在斜面上还能滑行的时间和距离分别为

5m

3Bqtanθ

和

35m2gcos2θ

12B2q2sinθ

．

点评：本题分析滑块的受力情况，判断其运动情况是关键，把握住临界条件，根据动能定理求距离，根据动量定理求时间是常用的思路．