题目内容
（2013?安徽）如图所示，细线的一端系一质量为m的小球，另一端固定在倾角为θ的光滑斜面体顶端，细线与斜面平行．在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，小球受到细线的拉力T和斜面的支持力为FN分别为（重力加速度为g）（ ）分析：小球始终静止在斜面上，说明斜面体加速度很小，且未脱离斜面，以小球受力分析，利用牛顿第二定律列式求解即可．
解答：解：当加速度a较小时，小球与斜面一起运动，此时小球受重力、绳子拉力和斜面的支持力，绳子平行于斜面；小球的受力如图：
水平方向上
由牛顿第二定律得：Tcosθ-FNsinθ=ma ①
竖直方向上
由平衡得：Tsinθ+FNcosθ=mg ②
①②联立得：FN=m（gcosθ-asinθ） T=m（gsinθ+acosθ） 故A正确，BCD错误．
故选A．
水平方向上
由牛顿第二定律得：Tcosθ-FNsinθ=ma ①
竖直方向上
由平衡得：Tsinθ+FNcosθ=mg ②
①②联立得：FN=m（gcosθ-asinθ） T=m（gsinθ+acosθ） 故A正确，BCD错误．
故选A．
点评：此题最难解决的问题是小球是否飞离了斜面，我们可以用假设法判断出临界加速度来进行比较．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
（2013?安徽）如图所示，足够长平行金属导轨倾斜放置，倾角为37°，宽度为0.5m，电阻忽略不计，其上端接一小灯泡，电阻为1Ω．一导体棒MN垂直于导轨放置，质量为0.2kg，接入电路的电阻为1Ω，两端与导轨接触良好，与导轨间的动摩擦因数为0.5．在导轨间存在着垂直于导轨平面的匀强磁场，磁感应强度为0.8T．将导体棒MN由静止释放，运动一段时间后，小灯泡稳定发光，此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为（重力加速度g取10m/s2，sin37°=0.6）（ ）
（2013?安徽模拟）如图所示，倾角为θ的足够长的粗糙斜面固定在水平地面上，质量为M的木块上固定一轻直角支架，在支架末端用轻绳悬挂一质量为m的小球．由静止释放木块，木块沿斜面下滑，稳定后轻绳与竖直方向夹角为a，则木块与斜面间的动摩擦因数为（ ）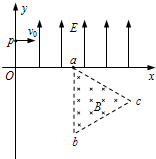
（2013?安徽）如图所示的平面直角坐标系xOy，在第Ⅰ象限内有平行于y轴的匀强电场，方向沿y正方向；在第Ⅳ象限的正三角形abc区域内有匀强磁场，方向垂直于xOy平面向里，正三角形边长为L，且ab边与y轴平行．一质量为m、电荷量为q的粒子，从y轴上的p（0，h）点，以大小为v0的速度沿x轴正方向射入电场，通过电场后从x轴上的a（2h，0）点进入第Ⅳ象限，又经过磁场从y轴上的某点进入第Ⅲ象限，且速度与y轴负方向成45°角，不计粒子所受的重力．求：
（2013?安徽）如图所示，质量为M倾角为α的斜面体（斜面光滑且足够长）放在粗糙的水平地面上，底部与地面的动摩擦因数为μ，斜面顶端与劲度系数为k、自然长度为l的轻质弹簧相连，弹簧的另一端连接着质量为m的物块．压缩弹簧使其长度为