题目内容
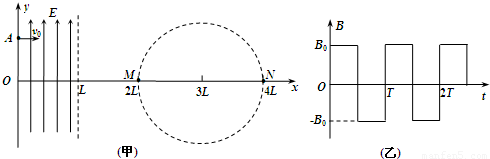
如图(甲)所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,右侧有一个以点(3L,0)为圆心、半径为L的圆形区域,圆形区域与x轴的交点分别为M、N.现有一质量为m,带电量为e的电子,从y轴上的A点以速度v沿x轴正方向射入电场,飞出电场后从M点进入圆形区域,速度方向与x轴夹角为30°.此时在圆形区域加如图(乙)所示周期性变化的磁场,以垂直于纸面向外为磁场正方向),最后电子运动一段时间后从N飞出,速度方向与进入磁场时的速度方向相同(与x轴夹角也为30°).求:(1)电子进入圆形磁场区域时的速度大小;
(2)0≤x≤L区域内匀强电场场强E的大小;
(3)写出圆形磁场区域磁感应强度B的大小、磁场变化周期T各应满足的表达式.
【答案】分析:电子在电场中只受电场力,做类平抛运动.将速度分解,可求出电子进入圆形磁场区域时的速度大小.根据牛顿定律求出场强E的大小.电子在磁场中,洛伦兹力提供向心力,做匀速圆周运动.分析电子进入磁场的速度方向与进入磁场时的速度方向相同条件,根据圆的对称性,由几何知识得到半径,周期T各应满足的表达式.
解答: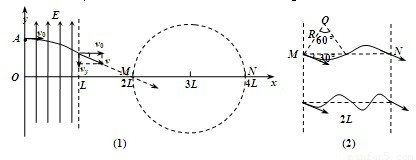
解:
(1)电子在电场中作类平抛运动,射出电场时,如图1所示.
由速度关系: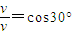 解得
解得 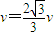
(2)由速度关系得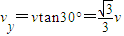
在竖直方向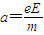
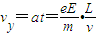
解得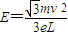
(3)在磁场变化的半个周期内粒子的偏转角为60°,根据几何知识,在磁场变化的半个周期内,
粒子在x轴方向上的位移恰好等于R.粒子到达N点而且速度符合要求的空间条件是:2nR=2L
电子在磁场作圆周运动的轨道半径
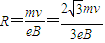
解得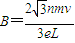 (n=1、2、3…)
(n=1、2、3…)
若粒子在磁场变化的半个周期恰好转过 圆周,同时MN间运动时间是磁场变化周期的整数倍时,
圆周,同时MN间运动时间是磁场变化周期的整数倍时,
可使粒子到达N点并且 速度满足题设要求.应满足的时间条件:
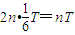 解得
解得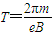
T的表达式得: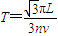 (n=1、2、3…)
(n=1、2、3…)
答:(1)电子进入圆形磁场区域时的速度大小为解得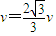 ;
;
(2)0≤x≤L区域内匀强电场场强E的大小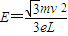 ;
;
(3)圆形磁场区域磁感应强度B的大小表达式为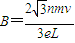 (n=1、2、3…)
(n=1、2、3…)
磁场变化周期T各应满足的表达式为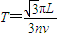 (n=1、2、3…).
(n=1、2、3…).
点评:本题带电粒子在组合场中运动,分别采用不同的方法:电场中运用运动的合成和分解,磁场中圆周运动处理的基本方法是画轨迹.所加磁场周期性变化时,要研究规律,得到通项.
解答:

解:
(1)电子在电场中作类平抛运动,射出电场时,如图1所示.
由速度关系:
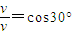 解得
解得 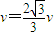
(2)由速度关系得
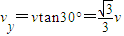
在竖直方向
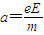
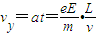
解得
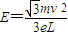
(3)在磁场变化的半个周期内粒子的偏转角为60°,根据几何知识,在磁场变化的半个周期内,
粒子在x轴方向上的位移恰好等于R.粒子到达N点而且速度符合要求的空间条件是:2nR=2L
电子在磁场作圆周运动的轨道半径
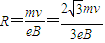
解得
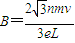 (n=1、2、3…)
(n=1、2、3…) 若粒子在磁场变化的半个周期恰好转过
 圆周,同时MN间运动时间是磁场变化周期的整数倍时,
圆周,同时MN间运动时间是磁场变化周期的整数倍时,可使粒子到达N点并且 速度满足题设要求.应满足的时间条件:
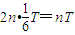 解得
解得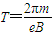
T的表达式得:
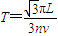 (n=1、2、3…)
(n=1、2、3…)答:(1)电子进入圆形磁场区域时的速度大小为解得
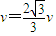 ;
;(2)0≤x≤L区域内匀强电场场强E的大小
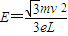 ;
;(3)圆形磁场区域磁感应强度B的大小表达式为
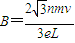 (n=1、2、3…)
(n=1、2、3…) 磁场变化周期T各应满足的表达式为
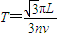 (n=1、2、3…).
(n=1、2、3…).点评:本题带电粒子在组合场中运动,分别采用不同的方法:电场中运用运动的合成和分解,磁场中圆周运动处理的基本方法是画轨迹.所加磁场周期性变化时,要研究规律,得到通项.

练习册系列答案
相关题目
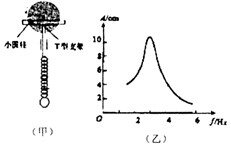 如图(甲)所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统.当圆盘静止时,小球可稳定振动.现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定.改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图(乙)所示,则( )
如图(甲)所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统.当圆盘静止时,小球可稳定振动.现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定.改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图(乙)所示,则( )| A、此振动系统的固有频率约为3Hz | B、此振动系统的固有频率约为0.25Hz | C、若圆盘匀速转动的周期增大,系统的振动频率不变 | D、若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动 |
 如图(甲)所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统.当圆盘静止时,小球可稳定振动.现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定.改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图(乙)所示,则( )
如图(甲)所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统.当圆盘静止时,小球可稳定振动.现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定.改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图(乙)所示,则( )| A、此振动系统的固有频率约为3Hz | B、此振动系统的固有频率约为0.25Hz | C、若圆盘匀速转动的周期增大,振动系统的固有频率不变 | D、若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动 |
 如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.
如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.
 如图(甲)所示,在竖直向下的B=5T的有界匀强磁场中,有一个边长为0.4m的正方形闭合金属线框放在光滑水平地面上,线框的ab边与磁场右边界MN平行且相距0.09m,线框电阻为10Ω、质量为0.20kg,t=0时,线框静止.现对线框加一向右的水平拉力F,使线框以a=2.0m/s2的加速度做匀加速直线运动,试通过分析和计算,在图(乙)上画出F-t 图线.
如图(甲)所示,在竖直向下的B=5T的有界匀强磁场中,有一个边长为0.4m的正方形闭合金属线框放在光滑水平地面上,线框的ab边与磁场右边界MN平行且相距0.09m,线框电阻为10Ω、质量为0.20kg,t=0时,线框静止.现对线框加一向右的水平拉力F,使线框以a=2.0m/s2的加速度做匀加速直线运动,试通过分析和计算,在图(乙)上画出F-t 图线.