题目内容
如图所示，第三象限内存在互相垂直的匀强电场和匀强磁场，匀强磁场方向向里，大小为B0，匀强电场场强为E。第二象限的某个矩形区域内，有方向垂直纸面向内的匀强磁场，磁场的下边界与x轴重合。一质量为m、电荷量为q的带正电粒子，以某一速度从M点进入第三象限，沿与y轴成600的直线运动到P点，在P点进入第二象限的磁场，经过一段时间后粒子垂直y轴上的N点通过y轴，N点到原点距离为L。忽略粒子的重力影响。求：
（1）请分析匀强电场的场强方向并求出粒子的运动速度。（6分）
（2）矩形有界磁场的磁感应强度B的大小。（10分）
（3）矩形有界磁场的最小面积。（4分）（要求有必要的文字叙述和轨迹图）
【答案】
略
【解析】（1）由于不计重力，粒子在第三象限内运动时只受电场力和洛伦兹力，它的运动为匀速直线运动，根据左手定则带正电的粒子受洛伦兹力方向垂直MP斜向下，电场力与洛伦兹力平衡斜向上，与y轴负方向成300角。 3分
由平衡条件有：
2分
所以 
1分
（2）粒子在第二象限运动轨迹如图。----- 2分
由几何关系得
3分
根据牛顿第二定律有
2分
解得 
3分
（3）有节磁场的最小面积
4分
练习册系列答案
相关题目
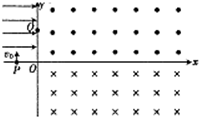（2011?安徽三模）如图所示，在第二象限内有水平向右的匀强电场，在第一、第四象限内分别存在匀强磁场，磁感应强度大小相等，方向如图所示；现有一个带电粒子在该平面内从x轴上的P点，以垂直于x轴初速度v0进入匀强电场，恰好经过y轴上的Q点且与y轴成45°角射出电场，再经过一段时间又恰好垂直于x轴进入下面的磁场．已知OP之间的距离为d，（不计粒子的重力）求：
