题目内容
14.如图甲所示,相距d的两根足够长的金属制成的导轨,水平部分左端ef间连接一阻值为2R的定值电阻,并用电压传感器实际监测两端电压,倾斜部分与水平面夹角为37°.长度也为d、质量为m的金属棒ab电阻为R,通过固定在棒两端的金属轻滑环套在导轨上,滑环与导轨上MG、NH段动摩擦因数μ=$\frac{1}{8}$(其余部分摩擦不计).MN、PQ、GH相距为L,MN、PQGH相距为L,MN、PQ间有垂直轨道平面向下、磁感应强度为B1的匀强磁场,PQ、GH间有平行于斜面但大小、方向未知的匀强磁场B2,其他区域无磁场,除金属棒及定值电阻,其余电阻均不计,sin37°=0.6,cos37°=0.8,当ab棒从MN上方一定距离由静止释放通过MN、QP区域(运动过程ab棒始终保护水平),电压传感器监测到U-t关系如图乙所示: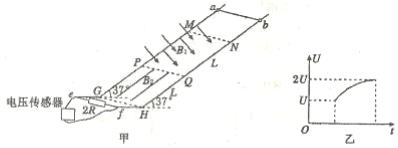
(1)求ab棒刚进入磁场B1时的速度大小;
(2)求定值电阻上产生的热量Q1;
(3)多次操作发现,当ab棒从MN以某一特定速度进入MNQP区域的同时,另一质量为2m、电阻为2R的金属棒cd只要以等大速度从PQ进入PQHG区域,两棒均匀速同时通过各自场区,试求B2的大小和方向.
分析 (1)根据电压传感器的示数求解感应电动势,根据导体切割磁感线产生的感应电动势计算公式求解速度大小;
(2)根据图乙可得ab杆匀速运动时定值电阻两端电压,根据闭合电路的欧姆定律和法拉第电磁感应定律求解速度大小,根据动能定理求解产生的总热量,根据焦耳定律可得定值电阻产生的焦耳热;
(3)两棒以相同的初速度进入场区,匀速经过相同的位移,分别对对ab棒、cd棒根据共点力平衡条件列方程求解B2,根据左手定则判断B2方向.
解答 解:(1)根据ab棒刚进入磁场B1时电压传感器的示数为U可得此时的感应电动势E1=U+$\frac{U}{2R}•R$=1.5U,
根据导体切割磁感线产生的感应电动势计算公式可得:E1=B1dv1
解得:v1=$\frac{1.5U}{{B}_{1}d}$;
(2)设金属棒ab离开PQ时的速度为v2,根据图乙可知,定值电阻两端电压为2U,
根据闭合电路的欧姆定律可得:$\frac{{B}_{1}d{v}_{2}}{2R+R}•2R=2U$,
解得:v2=$\frac{3U}{{B}_{1}d}$;
棒ab从MN到PQ,根据动能定理可得:
mgsin37°•L-μmgcos37°•L-W安=$\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}$
根据功能关系可得产生的总的焦耳热Q总=W安,
根据焦耳定律可得定值电阻产生的焦耳热为Q1=$\frac{2R}{2R+R}{Q}_{总}$
联立解得Q1=$\frac{1}{3}mgL-\frac{9m{U}^{2}}{4{B}_{1}^{2}{d}^{2}}$;
(3)两棒以相同的初速度进入场区,匀速经过相同的位移,对ab棒,根据共点力的平衡可得:
mgsin37°-μmgcos37°-$\frac{{B}_{1}^{2}{d}^{2}v}{2R}$=0,
解得:v=$\frac{mgR}{{B}_{1}^{2}{d}^{2}}$;
对cd棒,因为2mgsin37°-μ•2mgcos37°>0,故cd棒安培力必须垂直导轨平面向下,
根据左手定则可知磁感应强度B2沿导轨平面向上,cd棒也匀速运动,则有:
$2mgsin37°-μ(2mgcos37°+{B}_{2}×\frac{1}{2}×\frac{{B}_{1}dv}{2R}×d)=0$,
将v=$\frac{mgR}{{B}_{1}^{2}{d}^{2}}$代入解得:B2=32B1.
答:(1)ab棒刚进入磁场B1时的速度大小为$\frac{1.5U}{{B}_{1}d}$;
(2)定值电阻上产生的热量为$\frac{1}{3}mgL-\frac{9m{U}^{2}}{4{B}_{1}^{2}{d}^{2}}$;
(3)B2的大小为32B1,方向沿导轨平面向上.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 如图,P为处于水平面内的转盘,可绕竖直转轴OO′转动,长度为l的缆绳一端悬挂在转盘边缘,另一端栓接一质量为m的小球,转盘静止时缆绳与转轴间的距离为d,现让转盘由静止逐渐加速转动,经过一段时间后小球与转盘一起做匀速圆周运动,且缆绳与转轴在同一竖直面内,此时缆绳与竖直方向的夹角为θ,不计空气阻力以及缆绳重力,重力加速度为g,下列判断正确的是( )
如图,P为处于水平面内的转盘,可绕竖直转轴OO′转动,长度为l的缆绳一端悬挂在转盘边缘,另一端栓接一质量为m的小球,转盘静止时缆绳与转轴间的距离为d,现让转盘由静止逐渐加速转动,经过一段时间后小球与转盘一起做匀速圆周运动,且缆绳与转轴在同一竖直面内,此时缆绳与竖直方向的夹角为θ,不计空气阻力以及缆绳重力,重力加速度为g,下列判断正确的是( )| A. | 小球与转盘一起做匀速圆周运动时,小球受到缆绳的拉力大小为mgcosθ | |
| B. | 小球从静止到做匀速圆周运动的过程中,缆绳对小球做的功为$\frac{1}{2}$mgdtanθ | |
| C. | 小球从静止到做匀速圆周运动的过程中,重力对小球做的功为-mgl(1-cosθ) | |
| D. | 如果圆盘稳定转动时的角速度不变,换一个质量更大的小球随其转动,稳定时缆绳与竖直方向的夹角变小 |
 如图所示,匀强电场中的A、B、C、D点构成一位于纸面内平行四边形,电场强度的方向与纸面平行,已知A、B两点的电势分别为φA=12V、φB=6V,则C、D两点的电势可能分别为( )
如图所示,匀强电场中的A、B、C、D点构成一位于纸面内平行四边形,电场强度的方向与纸面平行,已知A、B两点的电势分别为φA=12V、φB=6V,则C、D两点的电势可能分别为( )| A. | 9V、18V | B. | 9V、15V | C. | 0V、6V | D. | 6V、0V |

| A. | 这列波的周期为2s | B. | 这列波的振幅为4cm | ||
| C. | 此时x=4m处质点的速度为零 | D. | 此时x=4m处质点沿y轴正方向运动 |
| A. | 正电子在A点的电势能为3.2×10-16J | |
| B. | 负电子在A点的电势能为-3.2×10-16J | |
| C. | A点的电势为-2000V | |
| D. | A点的电势为2000V |
 小明同学利用如图甲所示的装置来验证机械能守恒定律.A为装有挡光片的钩码,总质量为M,挡光片的挡光宽度为b,轻绳一端与A相连,另一端跨过光滑轻质定滑轮与质量为M的重物B相连.保持A、B静止,测出A的挡光片下端到光电门的距离h,然后将质量为m的小物体放在A上(图中没有画出),A下落过程中经过光电门,光电门可测出挡光片的挡光时间t,算出挡光片经过光电门的平均速度.将其视为A下落h(h>>b)时的速度,重力加速度为g.
小明同学利用如图甲所示的装置来验证机械能守恒定律.A为装有挡光片的钩码,总质量为M,挡光片的挡光宽度为b,轻绳一端与A相连,另一端跨过光滑轻质定滑轮与质量为M的重物B相连.保持A、B静止,测出A的挡光片下端到光电门的距离h,然后将质量为m的小物体放在A上(图中没有画出),A下落过程中经过光电门,光电门可测出挡光片的挡光时间t,算出挡光片经过光电门的平均速度.将其视为A下落h(h>>b)时的速度,重力加速度为g. 如图所示,足够长的斜面上,质量均为m的两物块A、B相距l,B与斜面间无摩擦,A与斜面间动摩擦因素为?(?>tanθ),B由静止开始下滑,与A发生弹性碰撞,碰撞时间极短可忽略不计,碰后A开始下滑,设在本题中最大静摩擦力等于滑动摩擦力,重力加速度为g.求:
如图所示,足够长的斜面上,质量均为m的两物块A、B相距l,B与斜面间无摩擦,A与斜面间动摩擦因素为?(?>tanθ),B由静止开始下滑,与A发生弹性碰撞,碰撞时间极短可忽略不计,碰后A开始下滑,设在本题中最大静摩擦力等于滑动摩擦力,重力加速度为g.求: 在利用落体运动来验证机械能守恒定律的实验中,
在利用落体运动来验证机械能守恒定律的实验中,