题目内容
4. 如图所示,是一种电子扩束装置的原理示意图.直角坐标系原点O处有一电子发射装置,可以不断朝xOy平面内x≥0区域任意方向发射电子,电子的速率均为v0,已知电子的电荷量为e、质量为m.在0≤x≤d的区域内分布着沿x轴负方向的匀强电场,场强大小E=$\frac{3m{{v}_{0}}^{2}}{2ed}$,在x>d区域内分布着足够大且垂直于xOy平面向外的匀强磁场,磁感应强度大小B=$\frac{4m{v}_{0}}{ed}$,ab为一块很大的平面感光板,在磁场内平行于y轴放置,电子打到板上后会在板上形成一条亮线.不计电子的重力和电子之间的相互作用.求:
如图所示,是一种电子扩束装置的原理示意图.直角坐标系原点O处有一电子发射装置,可以不断朝xOy平面内x≥0区域任意方向发射电子,电子的速率均为v0,已知电子的电荷量为e、质量为m.在0≤x≤d的区域内分布着沿x轴负方向的匀强电场,场强大小E=$\frac{3m{{v}_{0}}^{2}}{2ed}$,在x>d区域内分布着足够大且垂直于xOy平面向外的匀强磁场,磁感应强度大小B=$\frac{4m{v}_{0}}{ed}$,ab为一块很大的平面感光板,在磁场内平行于y轴放置,电子打到板上后会在板上形成一条亮线.不计电子的重力和电子之间的相互作用.求:(1)电子进入磁场时速度v的大小;
(2)当感光板沿x轴方向移到某一位置时恰好没有电子打到板上,求板ab到y轴的距离x1;
(3)保持(2)中感光板位置不动,改变磁感应强度的大小,使所有电子都能打到感光板上,试计算此时最小的磁感应强度B′的大小.
分析 (1)电子在电场中运动时,电场力做功都相同,为eEd,根据动能定理求出电子离开电场时的速度大小,即得到电子进入磁场时速度的大小;
(2)电子进入磁场后由洛伦兹力充当向心力做匀速圆周运动.对于沿y轴负方向射出的电子进入磁场时,不能打到ab板上,则所有电子均不能打到ab板上.当此电子轨迹与ab板相切时,画出轨迹,由牛顿第二定律求出轨迹半径,由几何知识求出感光板到y轴的距离x1.
(3)沿y轴正方向射出的电子若能打到ab板上,则所有电子均能打到板上.此电子轨迹恰好与ab板相切,画出轨迹,由几何知识求出轨迹半径,由牛顿第二定律求解磁感应强度的大小.
解答 解:(1)电场力对电子做功,由动能定理得: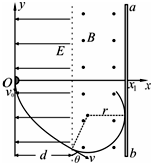
eEd=$\frac{1}{2}$mv2-$\frac{1}{2}$mv12,解得:v=2v1;
(2)由题意结合左手定则可以判定:若沿y轴负方向射出的电子进入磁场后轨迹与ab板相切不能打到ab板上时,
则所有电子均不能打到ab板上,作出其运动轨迹如图所示.
设该电子进入磁场时与竖直方向的夹角为θ,有:vcosθ=v1,
电子在洛伦兹力作用下做圆周运动,由牛顿第二定律得:evB=m$\frac{{v}^{2}}{r}$,
由图中几何关系可知:x1=r(1+cosθ)+d,解得:x1=$\frac{7}{4}$d;
(3)由题意结合左手定则可以判定:若沿y轴正方向射出的电子进入磁场后轨迹恰好与ab板相切能打到ab板上,
则所有电子均能打到板上,作出其运动轨迹如图所示.
由几何关系得:d+r′(1-cosθ)=r1,
由牛顿第二定律得:evB′=m$\frac{{v}^{2}}{r′}$,解得:B′=$\frac{4m{v}_{0}}{3ed}$;
答:(1)电子进入磁场时速度的大小为2v0;
(2)当感光板ab沿x轴方向移到某一位置时,恰好没有电子打到板上,感光板到y轴的距离x1为$\frac{7}{4}$d;
(3)保持(2)中感光板位置不动,若使所有电子恰好都能打到感光板上,磁感应强度的大小为:$\frac{4m{v}_{0}}{3ed}$.
点评 本题考查了粒子在电磁场中的运动问题,本题是电场中偏转和磁场中圆周运动的综合,关键是分析临界情况,当电子刚好不能打到ab板上时,其轨迹恰好与ab板相切,这是经常用到的临界条件.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 如图所示,轻质弹簧上端固定在天花板上,下端拴一小球.小球在重力和弹簧弹力的作用下沿竖直方向不停地往复运动,不计空气阻力,下列说法中正确的是( )
如图所示,轻质弹簧上端固定在天花板上,下端拴一小球.小球在重力和弹簧弹力的作用下沿竖直方向不停地往复运动,不计空气阻力,下列说法中正确的是( )| A. | 小球的机械能守恒 | |
| B. | 小球与弹簧组成的系统机械能守恒 | |
| C. | 弹簧处于原长时,小球的机械能最小 | |
| D. | 弹簧处于最长时,小球的机械能最小 |
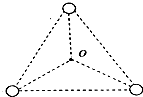 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )| A. | 每个星体受到向心力大小均为3$\frac{G{m}^{2}}{{a}^{2}}$ | |
| B. | 每个星体的角速度均为$\sqrt{\frac{3Gm}{{a}^{2}}}$ | |
| C. | 若a不变,m是原来的两倍,则周期是原来的$\frac{1}{2}$ | |
| D. | 若m不变,a是原来的4倍,则线速度是原来的$\frac{1}{2}$ |
| A. | 做直线运动 | B. | 做曲线运动 | ||
| C. | 可能做匀速圆周运动 | D. | 运动速度大小一定不断增大 |
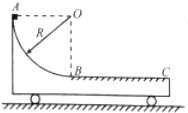 如图所示,质量为M=2kg的小车静止在光滑的水平地面上,其AB部分为半径R=0.5m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=1m,一质量m=1kg可看做质点的小物块从A点由静止释放,恰好能滑到C点,重力加速度取g=10m/s2,求:
如图所示,质量为M=2kg的小车静止在光滑的水平地面上,其AB部分为半径R=0.5m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=1m,一质量m=1kg可看做质点的小物块从A点由静止释放,恰好能滑到C点,重力加速度取g=10m/s2,求: