Question

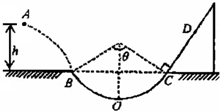如图所示，将一质量m=1kg的小物块以一定的初速度从A点水平抛出，恰好无碰撞地沿圆弧切线从B点进入光滑的竖直平面内圆弧轨道运动．圆弧的两端点B、C连线水平．小物块离开C点后恰能无碰撞地沿固定斜面向上运动，经0.8s通过D点．己知圆弧半径R=1.0m，圆弧对应的圆心角θ=106°，轨道最低点为O，A点距水平面的高度h=0.8m，小物块与斜面间的动摩擦因数μ=

1

3

，重力加速度g取10m/s²，sin37°=0.6，cos37°=0.8，试求：
（1）小物块离开A点的水平初速度υ_A；
（2）小物块经过O点时轨道的支持力大小N；
（3）斜面上C、D间的距离s_CD．

Answer 1

分析：（1）利用平抛运动规律，对B点的速度进行正交分解，得到水平速度和竖直方向速度的关系，
而竖直方向速度v_y=

2gh

，显然易求小物块离开A点的水平初速度υ_A；
（2）首先利用动能定理或机械能守恒求解物块在最低点O的速度，然后利用牛顿第二定律在最低点表示出向心力，则滑块受到的支持力可解．
（3）物块在轨道上上滑匀减速运动问题，要求出上滑的加速度、所需的时间；再求出下滑加速度、距离，利用匀变速直线运动规律公式求出位移差．根据牛顿第二定律和运动学公式求解．

解答：解：（1）对小物块，由A到B在竖直方向有  υ_y²=2gh
在B点tan

θ

2

=

vy

vA

      代入数据解得  υ_A=3m/s  
（2）小物块由B到O，根据机械能守恒定律得，
  mgR（1-cos

θ

2

）+

1

2

mυ_B²=

1

2

mυ_O²   
其中υ_B=

v 2 A + v 2 y

=5m/s       
小物块在O点，由牛顿笫二定律得  N-mg=m

v 2 O

R

  
代入数据解得    N=43N     
（3）小物块沿斜面上滑，由牛顿第二定律得  mgsin

θ

2

+μmgcos

θ

2

=ma₁
代入数据解得  a₁=10m/s²    
小物块沿斜面下滑，由牛顿第二定律得   mgsin

θ

2

-μmgcos

θ

2

=ma₂
代入数据解得  a₂=6m/s²    
由机械能守恒定律知  υ_C=υ_B=5m/s
小物块由C上升到最高点历时   t₁=

vc

a1

=0.5s       
小物块由最高点回到D点历时 t₂=0.8s-0.5s=0.3s
故s_CD=

0+vC

2

t₁-

1

2

a₂t₂²   
代入数据解得CD间的距离 s_CD=0.98m  
答：
（1）小物块离开A点的水平初速度υ_A是3m/s．
（2）小物块经过O点时轨道的支持力大小N是43N；
（3）斜面上C、D间的距离s_CD是0.98m．

点评：本题是一个单物体多过程的力学综合题，把复杂的过程分解成几个分过程是基本思路．关键是分析清楚物体的运动情况，然后根据动能定理、平抛运动知识、牛顿第二定律、向心力公式列式求解．