题目内容
14.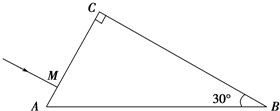 如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为,n=$\sqrt{2}$.在此截面所在的平面内,一条光线在距A点为$\frac{a}{8}$处的M点垂直AC射入棱镜,不考虑光线沿原路返回的情况,光线从玻璃砖的BC边射出.求:
如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为,n=$\sqrt{2}$.在此截面所在的平面内,一条光线在距A点为$\frac{a}{8}$处的M点垂直AC射入棱镜,不考虑光线沿原路返回的情况,光线从玻璃砖的BC边射出.求:①画出光路图
②光从棱镜射出时的折射角?;
③光从棱镜射出时的射出点距B多远?.
分析 ①设发生全反射的临界角为θC,由sin θC=$\frac{1}{n}$,得到θC=45°.由几何关系和临界条件判断出光线在AB上发生全反射,反射光线从CB折射出去.
②由几何关系求出光线在P点的入射角,由折射定律求出从CB射出时的折射角.
③由几何关系求解光从棱镜射出时的射出点距B的距离.
解答  解:①、②由图可知光线在N点的入射角 θ=60°,设发生全反射的临界角为θC,则sin θC=$\frac{1}{n}$,得θC=45°.
解:①、②由图可知光线在N点的入射角 θ=60°,设发生全反射的临界角为θC,则sin θC=$\frac{1}{n}$,得θC=45°.
由①可知,光在N点全反射,∠PNQ=30°,故光在P点的入射角为30°
设在P点的折射角为θ1,有$\frac{sin{θ}_{1}}{sin30°}$=n=$\sqrt{2}$ θ1=45°.
所以光路图如图,光从棱镜射出时的折射角是45°.
③由几何关系知AN=$\frac{a}{4}$,NB=$\frac{3a}{4}$,QB=$\frac{3a}{8}$
在三角形QPB中有cos30°=$\frac{QB}{PB}$,故PB=$\frac{QB}{cos30°}$=$\frac{\sqrt{3}}{4}$a.
答:(1)画出光路图如图.
(2)光从棱镜射出时的折射角45°.
(3)光从棱镜射出时的射出点距B距离为$\frac{\sqrt{3}}{4}$a.
点评 本题是折射定律、全反射和几何知识的综合应用,作出光路图,判断能否发生全反射是关键.

练习册系列答案
相关题目
2. 如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
 如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )| A. | 该波的传播速率为4 m/s | |
| B. | 该波的传播方向沿x轴正方向 | |
| C. | 经过0.5 s时间,质点P沿波的传播方向向前传播2 m | |
| D. | 该波在传播过程中若遇到8 m的障碍物,能发生明显衍射现象 |
6.下面关于行星绕太阳旋转的说法中正确的是( )
| A. | 离太阳越近的行星周期越大 | |
| B. | 离太阳越远的行星周期越小 | |
| C. | 离太阳越近的行星的向心加速度越大 | |
| D. | 以上说法都不对 |
3. 如图所示,闭合小金属环从高h的光滑曲面上端无初速滚下,又沿曲面的另一侧上升,水平方向的磁场与光滑曲面垂直,则( )
如图所示,闭合小金属环从高h的光滑曲面上端无初速滚下,又沿曲面的另一侧上升,水平方向的磁场与光滑曲面垂直,则( )
 如图所示,闭合小金属环从高h的光滑曲面上端无初速滚下,又沿曲面的另一侧上升,水平方向的磁场与光滑曲面垂直,则( )
如图所示,闭合小金属环从高h的光滑曲面上端无初速滚下,又沿曲面的另一侧上升,水平方向的磁场与光滑曲面垂直,则( )| A. | 若是匀强磁场,环在左侧滚上的高度小于h | |
| B. | 若是匀强磁场,环在左侧滚上的高度等于h | |
| C. | 若是非匀强磁场,环在左侧滚上的高度小于h | |
| D. | 若是非匀强磁场,环在左侧滚上的高度等于h |
 在贝克勒尔发现天然放射现象后,人们对三种放射线的性质进行了深入研究,如图为三种射线在同一磁场中的运动轨迹,判断射线名称:
在贝克勒尔发现天然放射现象后,人们对三种放射线的性质进行了深入研究,如图为三种射线在同一磁场中的运动轨迹,判断射线名称: 如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求:
如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求: 如图,有一个半径为R的圆弧形轨道,滑块A、B分别从轨道上面和下面沿轨道滑动,如果要求它们在最高点处不离开轨道,对它们在最高点的速率有什么限制?
如图,有一个半径为R的圆弧形轨道,滑块A、B分别从轨道上面和下面沿轨道滑动,如果要求它们在最高点处不离开轨道,对它们在最高点的速率有什么限制?