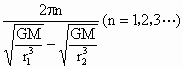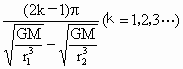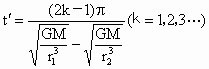题目内容
A、B两行星在同一平面内绕同一恒星做匀速圆周运动,运行方向相同,A的轨道半径为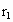 ,B的轨道半径为
,B的轨道半径为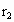 .已知恒星质量为M,恒星对行星的引力远大于行星间的引力,两行星的轨道半径
.已知恒星质量为M,恒星对行星的引力远大于行星间的引力,两行星的轨道半径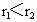 .若在某一时刻两行星相距最近,试求:
.若在某一时刻两行星相距最近,试求:
(1)再经过多少时间两行星距离又最近?
(2)再经过多少时间两行星距离最远?
答案:略
解析:
解析:
|
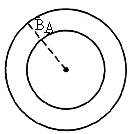
(1) (2) (1)A 、B两行星在如图所示位置时距离最近,这时A、B与恒星在同一条圆半径上,A、B运动方向相同,A更靠近恒星,A的转动角速度大、周期短,如果经过时间t,A、B与恒星连线半径转过的角度相差2π的整数倍,则A、B与恒星又位于同一条圆半径上,距离最近.设A、B的角速度分别为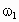 、 、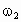 ,经过时间t,A转过的角度为 ,经过时间t,A转过的角度为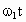 ,B转过的角度为 ,B转过的角度为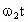 ,A、B距离最近的条件是: ,A、B距离最近的条件是: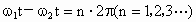
恒星对行星的万有引力提供向心力,则 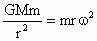 ,即 ,即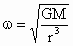
由此得出 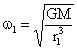 , ,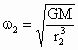
求得 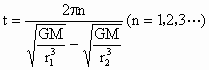
(2) 如果经过时间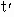 ,A、B转过的角度相差π的奇数倍时,则A、B相距最远,即: ,A、B转过的角度相差π的奇数倍时,则A、B相距最远,即: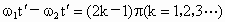
得 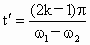 把 把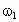 、 、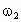 代入得: 代入得:
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目