题目内容
8. 如图所示,轻绳的一端固定在小车支架上,另一端拴着两个质量不同的小球.当小车水平向右运动且两段轻绳与竖直方向的夹角始终均为θ的过程中,若不计空气阻力,下列说法正确的是( )
如图所示,轻绳的一端固定在小车支架上,另一端拴着两个质量不同的小球.当小车水平向右运动且两段轻绳与竖直方向的夹角始终均为θ的过程中,若不计空气阻力,下列说法正确的是( )| A. | 两个小球的加速度不相等 | B. | 两段轻绳中的张力可能相等 | ||
| C. | 小车的速度越大,θ越大 | D. | 小车的加速度越大,θ越大 |
分析 小车和小球具有相同的加速度,对两小球分析,根据牛顿第二定律得出加速度的大小、拉力大小.
解答 解:AD、对两球整体受力分析,受到重力、拉力,
水平方向:T1sinθ=(m1+m2)a
竖直方向:T1cosθ-(m1+m2)g=0
解得:${T}_{1}=\frac{{m}_{1+}{m}_{2}}{cosθ}g$,a=gtanθ,两球加速度相等,可知小车的加速度越大,θ越大,A错误,D正确;
B、对下面小球m2,竖直方向:T2cosθ-m2g=0
解得:${T}_{2}=\frac{{m}_{2}}{cosθ}g$,可知T1>T2,即上段轻绳中的张力大于下段轻绳中的张力,B错误;
C、夹角θ与小车的速度无关,C错误;
故选:D.
点评 本题为牛顿第二定律中的连接体问题;解决本题的关键知道小球和小车具有相同的加速度,隔离对小球分析,运用牛顿第二定律进行求解;

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.关于磁电式电流表的工作原理,正确的说法是( )
| A. | 通电线圈受到的磁力矩与电流成正比 | |
| B. | 线圈受到的弹簧的反力矩与线圈转过的角度成正比 | |
| C. | 线圈内通过的电流方向改变时,线圈转动方向仍不变 | |
| D. | 电流增大时线圈转动的角度不变 |
16.从地面竖直向上抛出一个物体A,空气阻力不计,同时在离地面某一高度处另有一物体B开始自由下落,两物体在空中同时到达同一高度时速率都为v.则下述正确的是( )
| A. | 物体A上抛的初速度大小和B物体落地时的速度大小都是2v | |
| B. | 物体A和B落地时间相同 | |
| C. | 物体A能上升的最大高度和物体B开始下落时的高度相同 | |
| D. | 两物体在空中达同一个高度处,一定是B物体开始下落时的高度的中点 |
3.如图所示,两个截面积不同长度相等的均匀铜棒接在电路中,则( )
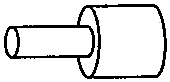

| A. | 相同时间内通过任一横截面的电荷量相等 | |
| B. | 相同时间内通过粗棒横截面的电荷量多 | |
| C. | 细棒与粗棒两端的电压相等 | |
| D. | 细棒两端的电压大于粗棒两端的电压 |
13.关于电场线,下列说法中正确的是( )
| A. | 电场线总是从负电荷出发到正电荷终止的一系列曲线 | |
| B. | 电场线上各点的切线方向,表示该点电场强度的方向 | |
| C. | 电场中任何两条电场线可以相交 | |
| D. | 电场线是客观存在的 |
20. 如图所示,用绳跨过定滑轮牵引小船,设水的阻力不变,则在小船匀速靠岸的过程中( )
如图所示,用绳跨过定滑轮牵引小船,设水的阻力不变,则在小船匀速靠岸的过程中( )
 如图所示,用绳跨过定滑轮牵引小船,设水的阻力不变,则在小船匀速靠岸的过程中( )
如图所示,用绳跨过定滑轮牵引小船,设水的阻力不变,则在小船匀速靠岸的过程中( )| A. | 绳子的拉力减小 | B. | 绳子的拉力不变 | C. | 船所受浮力减小 | D. | 船所受浮力不变 |
18.运动员将铅球从A处以一初速度斜向上抛出,运动轨迹如图中虚线所示.则小球到达最高点B处时( )


| A. | 速度为零,加速度为零 | B. | 速度为零,加速度不为零 | ||
| C. | 速度不为零,加速度为零 | D. | 速度不为零,加速度不为零 |
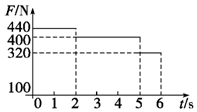 一质量为m=40kg的小孩站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.求在这段时间内电梯上升的高度是多少(取重力加速度g=10m/s2)
一质量为m=40kg的小孩站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.求在这段时间内电梯上升的高度是多少(取重力加速度g=10m/s2) 如图所示,劲度系数分别为k1、k2的两轻质弹簧与m1和m2两物体连接方式如图所示,系统处于静止,当用竖直向上的力F缓慢托起m2,当力F大小为m2g+$\frac{{k}_{2}{m}_{1}g}{{k}_{1}+{k}_{2}}$时,两弹簧的总长等于两弹簧原长之和.
如图所示,劲度系数分别为k1、k2的两轻质弹簧与m1和m2两物体连接方式如图所示,系统处于静止,当用竖直向上的力F缓慢托起m2,当力F大小为m2g+$\frac{{k}_{2}{m}_{1}g}{{k}_{1}+{k}_{2}}$时,两弹簧的总长等于两弹簧原长之和.