题目内容
8. 质谱仪的工作原理示意图如图所示,它由速度选择器和有边界的偏转磁场构成.速度选择器由两块水平放置的金属板构成,两金属板间的距离为d,上极板与电源正极相连,下极板与电源负极相连;板间匀强磁场的磁感应强度为B1,方向垂直纸面向里.偏转磁场为匀强磁场,磁感应强度的大小为B2,方向垂直纸面向外.当两金属板间的电势差为U时,一束带电粒子从狭缝O1射入,沿直线通过速度选择器,从磁场边界上的O2点垂直磁场方向射入偏转磁场,经历半个圆周打在照相底片上的A点,测得O2和A点之间的距离为L.粒子所受重力及粒子间的相互作用均可忽略.
质谱仪的工作原理示意图如图所示,它由速度选择器和有边界的偏转磁场构成.速度选择器由两块水平放置的金属板构成,两金属板间的距离为d,上极板与电源正极相连,下极板与电源负极相连;板间匀强磁场的磁感应强度为B1,方向垂直纸面向里.偏转磁场为匀强磁场,磁感应强度的大小为B2,方向垂直纸面向外.当两金属板间的电势差为U时,一束带电粒子从狭缝O1射入,沿直线通过速度选择器,从磁场边界上的O2点垂直磁场方向射入偏转磁场,经历半个圆周打在照相底片上的A点,测得O2和A点之间的距离为L.粒子所受重力及粒子间的相互作用均可忽略.(1)求带电粒子从速度选择器射出时的速度大小v.
(2)求带电粒子的比荷$\frac{q}{m}$.
(3)另外一束带电粒子也从狭缝O1射入,保持其他条件不变,粒子最终打在照相底片上的C点,O2和C点之间的距离大于L.比较这两束粒子,说明你能得到的结论,并阐述理由.
分析 (1)由于带电粒子做匀速直线运动,所以上平衡条件就能求出粒子的速度.
(2)测得O2和A点之间的距离为L,即粒子做匀速圆周运动的直径,由洛仑兹力提供向心力就能求出磁感应强度.
(3)另外一束带电粒子也从狭缝O1射入,保持其他条件不变,粒子最终打在照相底片上的C点,O2和C点之间的距离大于L,说明该粒子做匀速圆周运动的半径大,由左手定则等能够判断出该粒子的比荷大.
解答 解:(1)设带电粒子的电荷量为q,因为该粒子在金属板间做匀速直线运动,所以
qE=qvB1
又$E=\frac{U}{d}$
解得:$v=\frac{U}{{B}_{1}d}$
(2)带电粒子在偏转磁场中做匀速圆周运动,设圆周运动的半径为R,据牛顿第二定律
$qv{B}_{2}=m\frac{{v}^{2}}{R}$
又 $R=\frac{L}{2}$
解得:$\frac{q}{m}=\frac{2v}{{B}_{2}L}=\frac{2U}{{B}_{1}{B}_{2}Ld}$
(3)可得到的结论
①两束带电粒子都带正电荷.理由:根据左手定则判定两束带电粒子在偏转磁场中O2
点的受力方向都由O2指向A点.
②两束带电粒子的速度大小相等.理由:只有速度$v=\frac{U}{{B}_{1}d}$的带电粒子才能沿直线通过
速度选择器.
③打在C点的带电粒子的比荷小于打在A点的带电粒子的比荷.理由:带电粒子的比荷
$\frac{q}{m}=\frac{U}{{B}_{1}{B}_{2}Rd}$(式中R为带电粒子在偏转磁场中做匀速圆周运动的半径),而且打在
C点的带电粒子在偏转磁场中的半径大.
答:(1)求带电粒子从速度选择器射出时的速度大小为$\frac{U}{{B}_{1}d}$.
(2)求带电粒子的比荷为$\frac{2U}{{B}_{1}{B}_{2}Ld}$.
(3)另外一束带电粒子也从狭缝O1射入,保持其他条件不变,粒子最终打在照相底片上的
C点,O2和C点之间的距离大于L.比较这两束粒子,说明 ①两束带电粒子都带正电荷;
②两束带电粒子的速度大小相等;③打在C点的带电粒子的比荷小于打在A点的带电粒子的比荷.
点评 本题考察的是速度选择器和质谱仪的原理的综合,由平衡条件和牛顿第二定律就能求出相关的物理量.还要注意的是打在荧光屏上点距出发点的距离为粒子做匀速圆周运动半径的2倍即直径.

 巧学巧练系列答案
巧学巧练系列答案| A. | 物体发生形变时,其重心位置一定不变 | |
| B. | 物体升高时,只要物体的形状和质量分布情况不变,其重心在空中位置一定不变 | |
| C. | 将物体悬挂起来平衡时,重心必在悬挂点的正下方 | |
| D. | 形状规则的物体重心必在其几何中心处 |
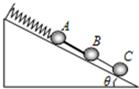 如图所示,A、B、C三球质量均为m,轻质弹簧一端固定在斜面顶端、另一端与A球相连,A、B间固定一个轻杆,B、C间由一轻质细线连接.倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )
如图所示,A、B、C三球质量均为m,轻质弹簧一端固定在斜面顶端、另一端与A球相连,A、B间固定一个轻杆,B、C间由一轻质细线连接.倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )| A. | A球的受力情况未变,加速度为零 | |
| B. | C球的加速度沿斜面向下,大小为$\frac{g}{2}$ | |
| C. | A、B之间杆的拉力大小为2mgsinθ | |
| D. | A、B两个小球的加速度均沿斜面向上,大小均为$\frac{1}{2}$gsinθ |


 如图所示,质量为m的带电小球用绝缘丝线悬挂于O点,并处在水平向左广大的匀强电场E中,小球静止时丝线与竖直方向夹角为θ,则小球的带电量为$\frac{mgtanθ}{E}$;若剪断丝线带电小球将沿绳方向向下做初速度为零的匀加速直线运动运动.
如图所示,质量为m的带电小球用绝缘丝线悬挂于O点,并处在水平向左广大的匀强电场E中,小球静止时丝线与竖直方向夹角为θ,则小球的带电量为$\frac{mgtanθ}{E}$;若剪断丝线带电小球将沿绳方向向下做初速度为零的匀加速直线运动运动.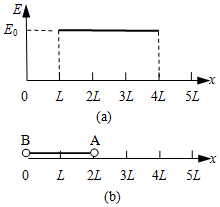 光滑绝缘水平面上有一水平向右的匀强电场,其场强大小分布如图(a)所示.两个质量均为m的带电小球A和B由长为2L的轻杆相连,组成一带电系统,球A带电量为+2q,球B带电量为-q.t=0时刻,带电系统由如图(b)所示位置从静止开始运动.若视小球为质点,不计轻杆的质量,求:
光滑绝缘水平面上有一水平向右的匀强电场,其场强大小分布如图(a)所示.两个质量均为m的带电小球A和B由长为2L的轻杆相连,组成一带电系统,球A带电量为+2q,球B带电量为-q.t=0时刻,带电系统由如图(b)所示位置从静止开始运动.若视小球为质点,不计轻杆的质量,求: