题目内容
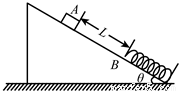
如图所示,固定斜面的倾角为θ,可视为质点的物体A与斜面之间的动摩擦因数为μ,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于B点.物体A的质量为m,开始时物体A到B点的距离为L.现给物体A一沿斜面向下的初速度v,使物体A开始沿斜面向下运动,物体A将弹簧压缩到最短后又恰好被弹回到B点.已知重力加速度为g,不计空气阻力,求此过程中:(1)物体A向下运动刚到达B点时速度的大小
(2)弹簧的最大压缩量.
【答案】分析:(1)对从最高点到第一次与弹簧接触过程运用动能定理列式求解即可;
(2)对从第一次接触弹簧到第二次接触弹簧过程直接运用动能定理列式求解.
解答:解:(1)物体A由开始运动直至B点的过程,由动能定理得 mgLsinθ-μmgLcosθ= mv B2-
mv B2- mv 02
mv 02
求得:vB=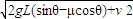
(2)设弹簧最大压缩量为x.在物体A刚好接触弹簧直至恰好返回到B点的过程中,由动能定理得(或功能关系)
-2μmg x cosθ=0- m
m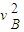
求得 x=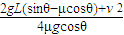 .
.
点评:本题关键是要灵活地选择物理过程运用动能定理列式求解,同时要明确弹簧弹力做的功等于弹性势能的变化.
(2)对从第一次接触弹簧到第二次接触弹簧过程直接运用动能定理列式求解.
解答:解:(1)物体A由开始运动直至B点的过程,由动能定理得 mgLsinθ-μmgLcosθ=
 mv B2-
mv B2- mv 02
mv 02 求得:vB=
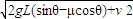
(2)设弹簧最大压缩量为x.在物体A刚好接触弹簧直至恰好返回到B点的过程中,由动能定理得(或功能关系)
-2μmg x cosθ=0-
 m
m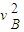
求得 x=
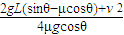 .
.点评:本题关键是要灵活地选择物理过程运用动能定理列式求解,同时要明确弹簧弹力做的功等于弹性势能的变化.

练习册系列答案
相关题目
 如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( )
如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( ) 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: 如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为
如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为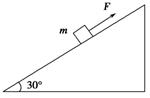
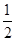 mg B.mg C.
mg B.mg C.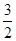 mg D.
mg D.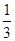 mg
mg 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: