题目内容
某人造卫星绕地球做匀速圆周运动,它离地面的高度为h,地球半径为R,地球质量为m1,引力常量为G,求:(1)卫星的线速度大小V;
(2)卫星的周期T;
(3)不考虑地球的自转,求地球表面的重力加速度大小g.
【答案】分析:(1)人造卫星绕地球做匀速圆周运动,由万有引力充当向心力可得出线速度的大小
(2)根据圆周运动的知识可得出周期的大小
(3)对地球表面的物体,根据万有引力等于重力求得地球表面的重力加速度大小.
解答:解:(1)人造卫星绕地球做匀速圆周运动,由万有引力充当向心力可得
对卫星,有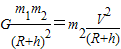
得卫星的线速度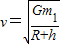
(2)根据圆周运动的知识得:
卫星的周期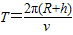
=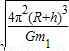
(3)对地球表面的物体,根据万有引力等于重力有
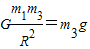
得重力加速度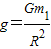
答:(1)卫星的线速度大小是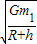 ;
;
(2)卫星的周期T是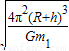 ;
;
(3)地球表面的重力加速度大小g是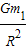 .
.
点评:人造地球卫星所受到的万有引力充当向心力,故由向心力公式可求得线速度、周期等.
万有引力定律的应用要结合圆周运动的知识解决问题.
(2)根据圆周运动的知识可得出周期的大小
(3)对地球表面的物体,根据万有引力等于重力求得地球表面的重力加速度大小.
解答:解:(1)人造卫星绕地球做匀速圆周运动,由万有引力充当向心力可得
对卫星,有
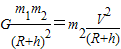
得卫星的线速度
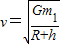
(2)根据圆周运动的知识得:
卫星的周期
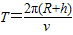
=
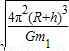
(3)对地球表面的物体,根据万有引力等于重力有
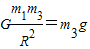
得重力加速度
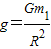
答:(1)卫星的线速度大小是
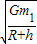 ;
;(2)卫星的周期T是
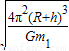 ;
;(3)地球表面的重力加速度大小g是
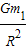 .
.点评:人造地球卫星所受到的万有引力充当向心力,故由向心力公式可求得线速度、周期等.
万有引力定律的应用要结合圆周运动的知识解决问题.

练习册系列答案
相关题目
设某人造卫星绕地球做匀速圆周运动,轨道半径为r.已知地球的质量为M,万有引力常量为G,该人造卫星与地心连线在单位时间内所扫过的面积是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、2
|