题目内容
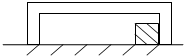 如图,质量m=2.0kg的滑块(可视为质点)放在水平面上,与水平面之间的动摩擦因数μ1=0.2,质量也为m=2.0kg的无底盒盖住滑块,盒长L=20cm,盒子与地面动摩擦因数μ2=0.1.现给盒子一个水平向右的初速度v0=10m/s,若盒子与滑块的碰撞是弹性的,试讨论盒子与滑块的碰撞次数.
如图,质量m=2.0kg的滑块(可视为质点)放在水平面上,与水平面之间的动摩擦因数μ1=0.2,质量也为m=2.0kg的无底盒盖住滑块,盒长L=20cm,盒子与地面动摩擦因数μ2=0.1.现给盒子一个水平向右的初速度v0=10m/s,若盒子与滑块的碰撞是弹性的,试讨论盒子与滑块的碰撞次数.分析:滑块与盒子在运动过程中要克服摩擦力做功,机械能减少,当克服摩擦力做功等于盒子的初动能时,盒子与滑块都静止;盒子与滑块碰撞过程中,系统动能守恒,应用动量守恒定律与动能定理分析答题.
解答:解:盒子与滑块的碰撞弹性碰撞,碰撞过程中系统动能守恒,机械能守恒,
以盒子与滑块组成的系统为研究对象,盒子的速度方向为正方向,
由动量守恒定律得:mv盒子=mv盒子′+mv滑块,
由机械能守恒定律得:
mv盒子2=
mv盒子′2+
mv滑块2,
解得:v盒子′=0,v滑块=v盒子,即,两者碰撞后相互交换速度;
盒子与滑块碰撞一次,盒子克服摩擦力做功:μ2mgL,
滑块与盒子碰撞一次,克服摩擦力做功μ1mgL,设盒子与滑块碰撞2n次,
对盒子与滑块在整个运动过程中,由动能定理得:
-nμ2mgL-nμ1mgL=0-
mv02
解得:n=
=
≈83.3,
则碰撞的次数2n=83.3×2=166.6,碰撞次数应取整数,则盒子与滑块碰撞的次数为166次;
答:盒子与滑块的碰撞次数为166次.
以盒子与滑块组成的系统为研究对象,盒子的速度方向为正方向,
由动量守恒定律得:mv盒子=mv盒子′+mv滑块,
由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v盒子′=0,v滑块=v盒子,即,两者碰撞后相互交换速度;
盒子与滑块碰撞一次,盒子克服摩擦力做功:μ2mgL,
滑块与盒子碰撞一次,克服摩擦力做功μ1mgL,设盒子与滑块碰撞2n次,
对盒子与滑块在整个运动过程中,由动能定理得:
-nμ2mgL-nμ1mgL=0-
| 1 |
| 2 |
解得:n=
| ||
| 2gL(μ1+μ2) |
| 102 |
| 2×10×0.2×(0.2+0.1) |
则碰撞的次数2n=83.3×2=166.6,碰撞次数应取整数,则盒子与滑块碰撞的次数为166次;
答:盒子与滑块的碰撞次数为166次.
点评:盒子与滑块碰撞是完全弹性碰撞,应用动量守恒定律与机械能守恒定律求出,两者碰撞后交换速度是正确解题的前提与关键,应用动能定理即可正确解题.

练习册系列答案
相关题目
 如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为 (2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
(2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为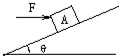 如图,质量m=2.5kg的物体A,在水平推力F的作用下,恰能沿倾角为θ=37°的斜面匀速上滑,g取10m/s2.
如图,质量m=2.5kg的物体A,在水平推力F的作用下,恰能沿倾角为θ=37°的斜面匀速上滑,g取10m/s2.