题目内容
如图所示，铜棒ab长0.1m，质量为0.06kg，两端由两根长都是1m的轻铜线悬挂起来，铜棒ab保持水平，整个装置静止于竖直平面内，装置所在处有竖直向下的匀强磁场，磁感应强度B=0.5T，现给铜棒ab中通入恒定电流，铜棒发生摆动．已知最大偏转角为37°，则铜棒从最低点运动到最高点的过程中，安培力做的功是 J，恒定电流的大小为 A（不计感应电流影响）．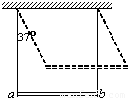
【答案】分析：铜棒从最低点运动到最高点的过程中，安培力做正功，重力做负功为-mgl（1-cos37°），根据动能定理求解安培力做的功．安培力做功为BIl?lsin37°，求出电流大小．
解答：解：铜棒从最低点运动到最高点的过程中，根据动能定理得：
W-mgl（1-cos37°）=0
得到W=mgl（1-cos37°）=0.06×10×1×0.2J=0.12J
又W=BIlab?lsin37°，代入解得I=4A．
故答案为：0.12，4
点评：动能定理是求功常用的方法，特别是变力做功．本题中安培力是恒力，可以运用功的计算公式求电流．
解答：解：铜棒从最低点运动到最高点的过程中，根据动能定理得：
W-mgl（1-cos37°）=0
得到W=mgl（1-cos37°）=0.06×10×1×0.2J=0.12J
又W=BIlab?lsin37°，代入解得I=4A．
故答案为：0.12，4
点评：动能定理是求功常用的方法，特别是变力做功．本题中安培力是恒力，可以运用功的计算公式求电流．
练习册系列答案
名校课堂系列答案
相关题目
（2009?上海模拟）如图所示，铜棒ab长0.1m，质量为0.06kg，两端与长为0.15m的轻铜线相连，静止于竖直平面上，整个装置处在竖直向下的匀强磁场中，磁感应强度为B=0.5T，现接通电源，使铜棒中保持有恒定电流通过，铜棒发生摆动．已知最大偏转角为37°，则在摆到最大偏角的过程中铜棒的重力势能增加了
（2011?静安区一模）如图所示，铜棒ab长0.1m，质量为0.06kg，两端由两根长都是1m的轻铜线悬挂起来，铜棒ab保持水平，整个装置静止于竖直平面内，装置所在处有竖直向下的匀强磁场，磁感应强度B=0.5T，现给铜棒ab中通入恒定电流，铜棒发生摆动．已知最大偏转角为37°，则铜棒从最低点运动到最高点的过程中，安培力做的功是
如图所示，铜棒ab长为0.5m，质量0.6Kg，两端用轻铜线相连．整个装置处在竖直向下的匀强磁场中，磁感应强度B=2T，接通电源，使铜棒中有恒定电流通过，若铜棒静止在与竖直方向成37°且偏向纸内的位置．求：铜棒中通过的电流大小和方向？
如图所示，铜棒ab长0.1m，质量为0.06kg，两端与长为0.15m的轻铜线相连，静止于竖直平面上，整个装置处在竖直向下的匀强磁场中，磁感应强度为B=0.5T，现接通电源，使铜棒中保持有恒定电流通过，铜棒发生摆动．已知最大偏转角为37°，则铜棒中的恒定电流的大小为