题目内容
在水平地面处,以30m/s的初速度竖直向上抛出一个小球,不计阻力.求:
(1)球距地面多高处,它的重力势能是动能的2倍?
(2)若小球在运动过程中,动能是重力势能的2倍时,它的速度多大?
(1)球距地面多高处,它的重力势能是动能的2倍?
(2)若小球在运动过程中,动能是重力势能的2倍时,它的速度多大?
分析:小球在上抛的过程中机械能守恒,由机械能守恒关系要得出重力势能为动能的两倍时的高度;同理可求得小球在运动过程中动能是重力势能的2倍时的速度大小.
解答:解:设地面为零势能面,则有:
(1)小球在运动过程中机械能守恒,则有机械能守恒可知
mv02=mgh+
mgh;
解得h=
=30m;
(2)由机械能守恒可知:
mv02=
mv2+
×
mv2;
解得:v=
=24.5m/s;
答:(1)球距地面30m处,它的重力势能是动能的2倍;(2)动能是重力势能的2倍时,它的速度为24.5m/s.
(1)小球在运动过程中机械能守恒,则有机械能守恒可知
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| ||
| 3 |
(2)由机械能守恒可知:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=
|
答:(1)球距地面30m处,它的重力势能是动能的2倍;(2)动能是重力势能的2倍时,它的速度为24.5m/s.
点评:本题考查机械能守恒定律的应用,注意设定零势能面,并且正确得出守恒的表达式.

练习册系列答案
相关题目
 如图所示,一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接,一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动.运动到B点时小滑块恰能沿光滑斜面下滑.已知AB间的距离s=5m,求:
如图所示,一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接,一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动.运动到B点时小滑块恰能沿光滑斜面下滑.已知AB间的距离s=5m,求: 如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在水平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑.g取10m/s2).某同学对此题的解法为:小球沿斜面运动,则
如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在水平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑.g取10m/s2).某同学对此题的解法为:小球沿斜面运动,则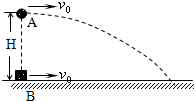 (2009?松江区二模)如图所示,在距地面高为H=45m处,有一小球A以初速度v0=10m/s水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度同方向滑出,B与水平地面间的动摩擦因数为μ=0.4,A、B均可视为质点,空气阻力不计.求A球落地时,A、B相距多远?某同学的解答如下:
(2009?松江区二模)如图所示,在距地面高为H=45m处,有一小球A以初速度v0=10m/s水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度同方向滑出,B与水平地面间的动摩擦因数为μ=0.4,A、B均可视为质点,空气阻力不计.求A球落地时,A、B相距多远?某同学的解答如下:
