题目内容
如图所示，A、B是两个摩擦传动轮，两轮半径大小关系为RA=2RB，则两轮边缘上的（ ）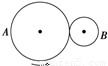
A．角速度之比ωA：ωB=2：1
B．周期之比TA：TB=1：2
C．转速之比nA：nB=1：2
D．向心加速度之比aA：aB=2：1
【答案】分析：解决本题的关键是两轮边缘上接触的地方线速度相等，然后根据角速度和线速度半径之间关系等求解．同时注意转速的物理意义，其在数值上和频率是相等的．
解答：解：两轮边缘的线速度相等，即vA=vB ①
线速度、角速度、半径关系为：v=ωr=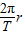
=2πnr ②
向心加速度为：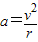
③
半径关系为：RA=2RB ④
联立①②③④可解得：ωA：ωB=1：2，TA：TB=2：1，nA：nB=1：2，aA：aB=1：2，故ABD错误，C正确．
故C正确．
点评：描述圆周运动的物理量较多如线速度、角速度、向心加速度、周期、频率、转速等，明确各物理量之间的关系，是解题的关键．
解答：解：两轮边缘的线速度相等，即vA=vB ①
线速度、角速度、半径关系为：v=ωr=
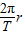=2πnr ②向心加速度为：
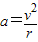③半径关系为：RA=2RB ④
联立①②③④可解得：ωA：ωB=1：2，TA：TB=2：1，nA：nB=1：2，aA：aB=1：2，故ABD错误，C正确．
故C正确．
点评：描述圆周运动的物理量较多如线速度、角速度、向心加速度、周期、频率、转速等，明确各物理量之间的关系，是解题的关键．
练习册系列答案
优生乐园系列答案
相关题目
如图所示，a、b是两个带有同种电荷的小球，现用两根绝缘细线将它们悬挂于真空中同一点．已知两球静止时，它们离水平地面的高度相等，线与竖直方向的夹角分别为α、β，且α＜β．现有以下判断，其中正确的是（ ）
如图所示，A、B是两块相同的均匀长方形砖块，质量为M，长度L，叠放在一起，且A相对于B的右端伸出
（2011?锦州模拟）如图所示，A、B是两个位于固定斜面上的正方体物块，它们的质量相等，F是沿水平方向作用于A上的外力，已知A与B的接触面，A、B与斜面的接触面均光滑，下列说法正确的是（ ）
如图所示，A，B是两个完全相同的灯泡，L是自感系数较大的线圈，其直流电阻忽略不计．当电键K闭合时，下列说法正确的是（ ）
电风扇的扇叶的重心如果不在转轴上，转动时会使风扇抖动，并加速转轴磨损．调整时，可在扇叶的一区域通过固定小金属块的办法改变其重心位置．如图所示，A、B是两调整重心的金属块（可视为质点），其质量相等，它们到转轴O的距离rA＜rB．扇叶转动后，它们的（ ）| A、向心力FA＜FB | B、线速度大小相等 | C、向心加速度相等 | D、角速度大小相等 |