题目内容
20.如图1所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰合与两个固定在地面上的压力传感器X和Y相接触,图AB高H=0.3m,AD长L=0.5m,斜面倾角θ=37°有一质量m=1kg的小物块p(图中未画出),它与斜面的动磨擦因数μ可以通过更换斜面的材料进行调节,调节范围是0≤μ≤1,取sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2.
(1)在A点给P一个沿斜面向上的初速度v0=3m/s,使之恰好能到达D点,求此时动摩擦因数μ的值;
(2)在第(1)问中若μ=0.5,求p落地时的动能;
(3)对于不同的μ,每次都在D点给p一个沿斜面向下足够大的初速度以保证它能滑离斜面.在p沿斜面下滑过程中,通过压力传感器能读出X或Y对大物块的水平压力F,取水平向左为正方向,试写出F随μ变化的关系表达式,并在坐标系中画出其函数图象.
分析 (1)对A到D过程,由动能定理可求得动摩擦因数μ的值;
(2)设上滑的位移为S,由动能定理可求得上滑的高度;对全程由动能定理可求得落地时的动能;
(3)对梯形物块进行受力分析,由共点力的平衡条件可求得F的表达式,根据表达式可画出图象.
解答  解:(1)小物块从A运动到D时速度为零,由动能定理得:
解:(1)小物块从A运动到D时速度为零,由动能定理得:
-(mgsinθ+μmgcosθ)L=0-$\frac{1}{2}$mv02
代入数据解得:μ=$\frac{3}{8}$=0.375;
(2)设小物块沿斜面上滑位移为S时速度为零,则由动能定理:
-(mgsinθ+μmgcosθ)s=0-$\frac{1}{2}$mv02;
代入数据解得:S=0.45m;
设落地时P的动能为EK,则由动能定理:
mgH-μmgcosθ•2S=EK-$\frac{1}{2}$mv02
代入数据解得:p落地时的动能 EK=3.9J;
(3)P在斜面上下滑的过程中,梯形物块的受力如图所示,设梯形物体块的质量为M.由平衡条件可得:
F+Nsinθ=fcosθ;
N=mgcosθ
又 f=μN=μmgcosθ;
联立以上三式,代入数据得:F=6.4μ-4.8;画出其函数图象如图.
答:(1)动摩擦因数为0.375;
(2)落地时的动能为3.9J;
(3)F随μ变化的关系表达式为F=6.4μ-4.8,图象如图.
点评 本题考查动能定理的应用,在解题时要正确进行受力分析,并且合理选择研究过程,找出正确的物理规律求解.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.在如图甲所示的电阻R上加上如图乙所示的交变电压,电表为理想交变电表( )


| A. | 交变电压周期是0.02s | |
| B. | 电压表读数为220V | |
| C. | 0.01s时,电流表读数为0 | |
| D. | 通过R的电流表达式为i=$\frac{220}{R}$sin100πt(A) |
11.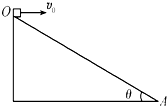 如图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中与斜面之间的最远距离( )•
如图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中与斜面之间的最远距离( )•
 如图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中与斜面之间的最远距离( )•
如图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中与斜面之间的最远距离( )•| A. | $\frac{{v}_{0}sinθ}{2g}$ | B. | $\frac{{{v}_{0}}^{2}}{2g}$ | ||
| C. | $\frac{{{v}_{0}}^{2}sinθ}{2gcosθ}$ | D. | $\frac{{{v}_{0}}^{2}si{n}^{2}θ}{2gcosθ}$ |
15.关于重心,下列说法中正确的是( )
| A. | 重心就是物体上最重的点 | |
| B. | 用一根细线悬挂的物体静止时,细线方向一定通过重心 | |
| C. | 重心的位置不一定在物体上,但形状规则的、质量分布均匀的物体的重心一定在物体上 | |
| D. | 质量分布均匀、形状规则的物体,它的重心在几何中心 |
5.如图所示,电磁铁P和Q通电后( )


| A. | P的右端是N极,Q的左端是S极,它们相互吸引 | |
| B. | P的右端是S极,Q的左端是S极,它们相互排斥 | |
| C. | P的右端是N极,Q的左端是N极,它们相互排斥 | |
| D. | P的右端是S极,Q的左端是N极,它们相互吸引 |
10.列关于物理学思想和方法的叙述错误的是( )
| A. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,再把各小段位移相加,这里运用了微元法 | |
| B. | 探究加速度与力和质量关系的实验运用了控制变量法 | |
| C. | 当物体的运动时间△t趋近于0时,△t时间内的平均速度可看成瞬时速度运用了等效替代法 | |
| D. | 奥斯特发现电生磁到法拉第发现磁生电的过程中运用了逆向思维法 |