题目内容
如图所示，长为L、内壁光滑的直管与水平地面成30°角固定位置．将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M＝3m的小物块相连，小物块悬挂于管口．现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变(重力加速度为g)。
求：(1)小物块下落过程中的加速度大小；
(2)小球从管口抛出时的速度大小；
(3)小球在做平抛过程中的水平位移。
(1)设细线中的张力为T，根据牛顿第二定律：
Mg－T＝Ma ①
T－mgsin30°＝ma ②
且M＝3m
解得a＝
g ③ （4分）
(2)设M落地时的速度大小为v，m射出管口时速度大小为v0，M落地后m的加速度为a0.根据牛顿第二定律有：
－mgsin30°＝ma0 ④ （2分）
又由匀变速直线运动，
v2＝2aLsin30°， ⑤ （2分）
v
－v2＝2a0L(1－sin30°) ⑥ （2分）
解得v0＝ 
⑦ （1分）
(3)平抛运动
x＝v0t ⑧ （1分）
Lsin30°＝
gt2 ⑨ （2分）
解得水平位移x＝
L ⑩ （2分）
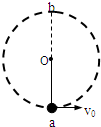如图所示，长为L的细绳一端与一质量为m的小球（可看成质点）相连，可绕过O点的水平转轴在竖直面内无摩擦地转动．在最低点a处给一个初速度，使小球恰好能通过最高点完成完整的圆周运动，求：
如图所示，长为L细绳一端固定于O点，另一端系一质量为m的小球并让小球以速度v在光滑水平面内做匀速圆周运动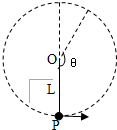
如图所示，长为L的轻绳一端固定在O点，另一端系一小球（可视为质点），小球在竖直平面内做逆时针方向的圆周运动，不计空气阻力．已知某次小球运动过程中通过传感器测得轻绳拉力T和竖直方向OP的夹角θ的关系满足T=b+bcosθ，b为已知的常数，当地重力加速度为g．则由此可知小球的质量为（ ）
（2011?东莞一模）如图所示，长为L的细绳一端固定，另一端系一质量为m的小球．给小球一个合适的初速度，小球便可在水平面内做匀速圆周运动，这样就构成了一个圆锥摆，设细绳与竖直方向的夹角为θ．下列说法中正确的是（ ）
如图所示，长为L的轻杆一端固定着质量为m的小球绕另一端O在竖直平面内做圆周运动，则下列说法中正确的是（ ）