题目内容
一质量M=0.8kg的中空的、粗细均匀的、足够长的绝缘细管,其内表面粗糙、外表面光滑;有一质量为m=0.2kg、电荷量为q=0.1C的带正电滑块以水平向右的速度进入管内,如图甲所示.细管置于光滑的水平地面上,细管的空间能让滑块顺利地滑进去,示意图如图乙所示.运动过程中滑块的电荷量保持不变.空间中存在垂直纸面向里的水平匀强磁场,磁感应强度为B=1.0T.(取水平向右为正方向,g=10m/s2)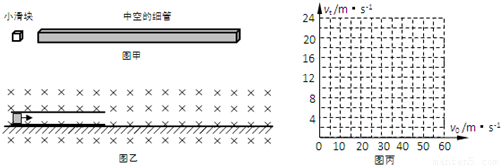
(1)滑块以v=10m/s的初速度进入细管内,则系统最终产生的内能为多少?
(2)滑块最终的稳定速度 vt取决于滑块进入细管时的初速度v
①请讨论当v的取值范围在0至60m/s的情况下,滑块和细管分别作什么运动,并求出vt和v的函数关系?
②以滑块的初速度v横坐标、滑块最终稳定时的速度vt为纵坐标,在丙图中画出滑块的vt-v图象(只需作出v的取值范围在0至60m/s的图象).
【答案】分析:(1)小滑块与细管组成的系统水平方向外力为零,因此水平方向系统动量守恒,然后根据功能关系即可求解.
(2)本问的关键是正确分析重力和洛伦兹力的关系,以重力等于洛伦兹力为临界点进行分析,当重力大于洛伦兹力时,细管下壁与滑块之间有支持力,当重力小于洛伦兹力时,细管上壁与滑块之间有支持力.明确了这些便找到了解决问题的突破点.
解答:解:(1)小球刚进入管内时受到洛仑兹力为:F洛=qvB=1N ①
依题意小球受洛仑兹力方向向上,F洛<mg=2N,小球与管的下壁有弹力,摩擦使球减速至最终与细管速度相同时,两者以共同速度v运动
由动量守恒定律:mv=(m+M)v ②
对系统:由能量守恒定律: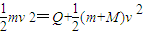 ③
③
由②③得:Q=8 J
故系统最终产生的内能为8J.
(2)①分析:当滑块对管的上下壁均无压力时,滑块进入细管的速度满足:mg=qv'B ④
得:v'=20m/s
下面分a、b两种情况进行讨论分析:
a、当滑块初速小于v=20m/s时,F洛<mg,滑块与管的下壁有弹力,并有摩擦力,使滑块作匀减速直线运动,细管作匀加速直线运动,最终两者共速
对系统:依动量守恒定律:mv=(m+M)vt ⑤
代入数据得:vt=0.2v0 ⑥(0<v<20m/s)
b、当滑块初速20m/s≤v≤60m/s时,滑块与管的上壁有弹力,摩擦使滑块减速最终速度为 vt=20m/s,而细管作匀加速直线运动,加速到V′⑧
当滑块以初速度为v进入,若恰好V′=vt=20m/s,则对系统依动量守恒定律有:mv=(m+M)V′
可得:v=100m/s>60m/s,
当滑块以v=60m/s进入时,f洛=qvB=6N<(m+m)g=10N
∴细管工不会离开地面.
可见:当滑块以初速度20m/s≤v≤60m/s进入细管时,细管最终不能加速到20m/s
故当滑块初速小于v=20m/s时,滑块作匀减速直线运动,细管作匀加速直线运动,最终两者以相同的速度一起匀速运动;
当滑块初速20m/s≤v≤60m/s时,滑块作匀减速直线运动,当速度达到20m/s时,开始运动运动,细管开始做匀加速运动,后做匀速运动,且速度小于20m/s.
②根据以上分析得出滑块的vt-v图象如下所示:
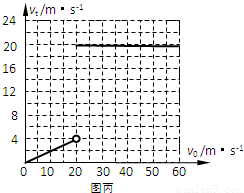
点评:本题过程、受力情况比较复杂,考查知识点全面,有一定难度,解答这类题目的关键是正确进行受力分析,弄清运动形式,然后依据规律求解.
(2)本问的关键是正确分析重力和洛伦兹力的关系,以重力等于洛伦兹力为临界点进行分析,当重力大于洛伦兹力时,细管下壁与滑块之间有支持力,当重力小于洛伦兹力时,细管上壁与滑块之间有支持力.明确了这些便找到了解决问题的突破点.
解答:解:(1)小球刚进入管内时受到洛仑兹力为:F洛=qvB=1N ①
依题意小球受洛仑兹力方向向上,F洛<mg=2N,小球与管的下壁有弹力,摩擦使球减速至最终与细管速度相同时,两者以共同速度v运动
由动量守恒定律:mv=(m+M)v ②
对系统:由能量守恒定律:
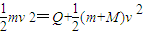 ③
③由②③得:Q=8 J
故系统最终产生的内能为8J.
(2)①分析:当滑块对管的上下壁均无压力时,滑块进入细管的速度满足:mg=qv'B ④
得:v'=20m/s
下面分a、b两种情况进行讨论分析:
a、当滑块初速小于v=20m/s时,F洛<mg,滑块与管的下壁有弹力,并有摩擦力,使滑块作匀减速直线运动,细管作匀加速直线运动,最终两者共速
对系统:依动量守恒定律:mv=(m+M)vt ⑤
代入数据得:vt=0.2v0 ⑥(0<v<20m/s)
b、当滑块初速20m/s≤v≤60m/s时,滑块与管的上壁有弹力,摩擦使滑块减速最终速度为 vt=20m/s,而细管作匀加速直线运动,加速到V′⑧
当滑块以初速度为v进入,若恰好V′=vt=20m/s,则对系统依动量守恒定律有:mv=(m+M)V′
可得:v=100m/s>60m/s,
当滑块以v=60m/s进入时,f洛=qvB=6N<(m+m)g=10N
∴细管工不会离开地面.
可见:当滑块以初速度20m/s≤v≤60m/s进入细管时,细管最终不能加速到20m/s
故当滑块初速小于v=20m/s时,滑块作匀减速直线运动,细管作匀加速直线运动,最终两者以相同的速度一起匀速运动;
当滑块初速20m/s≤v≤60m/s时,滑块作匀减速直线运动,当速度达到20m/s时,开始运动运动,细管开始做匀加速运动,后做匀速运动,且速度小于20m/s.
②根据以上分析得出滑块的vt-v图象如下所示:

点评:本题过程、受力情况比较复杂,考查知识点全面,有一定难度,解答这类题目的关键是正确进行受力分析,弄清运动形式,然后依据规律求解.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
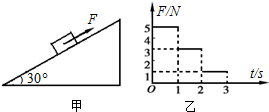 如图甲所示,倾角为30°的足够长的光滑斜面上,有一质量m=0.8kg的物体受到平行斜面向上的力F作用,其大小F随时间t变化的规律如图乙所示,t=0时刻物体速度为零,重力加速度g=10m/s2.下列说法中正确的是( )
如图甲所示,倾角为30°的足够长的光滑斜面上,有一质量m=0.8kg的物体受到平行斜面向上的力F作用,其大小F随时间t变化的规律如图乙所示,t=0时刻物体速度为零,重力加速度g=10m/s2.下列说法中正确的是( ) 如图竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高.一质量m=0.8kg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0.6,g取10/m2.试求:
如图竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高.一质量m=0.8kg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0.6,g取10/m2.试求: 如图甲所示,倾角为30°的足够长的光滑斜面上,有一质量m=0.8kg的物体受到平行斜面向上的力F作用,其大小F随时间t变化的规律如图乙所示,t=0时刻物体在斜面上的中点且速度为零,重力加速度g=10m/s2.下列说法中不正确的是( )
如图甲所示,倾角为30°的足够长的光滑斜面上,有一质量m=0.8kg的物体受到平行斜面向上的力F作用,其大小F随时间t变化的规律如图乙所示,t=0时刻物体在斜面上的中点且速度为零,重力加速度g=10m/s2.下列说法中不正确的是( )
 如图10所示,一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板土,处于静止状态.一质量m=0.2kg的橡皮泥粘性小球以速度v0=l0m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s2.求:
如图10所示,一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板土,处于静止状态.一质量m=0.2kg的橡皮泥粘性小球以速度v0=l0m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s2.求: