题目内容
9. 如图所示.粗糙水平面与半径R=1.6m的光滑$\frac{1}{4}$圆弧轨道相切于B点,质量为m=2kg的物体(可视为质点)从A点以遮度vA=6m/s向右运动.到达B点时的速度大小为VB=4m/s,g=10m/s2
如图所示.粗糙水平面与半径R=1.6m的光滑$\frac{1}{4}$圆弧轨道相切于B点,质量为m=2kg的物体(可视为质点)从A点以遮度vA=6m/s向右运动.到达B点时的速度大小为VB=4m/s,g=10m/s2(1)求从A到B的过程中,摩擦力对物体做的功:
(2)通过计算判断物体能否从圆轨道最高点飞出?
(3)若AB=5m.物体最终停在C点(图中未画出),则BC长度是多少?
分析 (1)以质点为研究对象,据动能定理求解即可.
(2)在圆弧中以质点为研究对象,利用机械能守恒求出上升的最大高度,在于半径相比较.
(3)整个运动过程为研究对象,利用能量守恒求解即可.
解答 解:(1)设摩擦力对物体为Wf,由动能定理得:
Wf=$\frac{1}{2}$mvB2-$\frac{1}{2}$mvA2
代入数据:Wf=-20J
(2)设物体从B进入圆轨道后,到达最高点离地高度为h,则
$\frac{1}{2}$mvB2=mgh
解得:h=0.8m
因为:h<R
所以:物体不会从圆轨道最高点飞出
(3)由于质点在圆弧上运动无摩擦力做功,设水平地面对物体的摩擦力为f
质点从A到B为研究过程,据动能定理:-fxAB=$\frac{1}{2}$mvB2-$\frac{1}{2}$mvA2
质点从B到C,由动能定理得:-fxBC=0-$\frac{1}{2}$mvB2
解得:xBC=4m
答:(1)求从A到B的过程中,摩擦力对物体做的功-20J:
(2)通过计算判断物体不能从圆轨道最高点飞出.
(3)若AB=5m.物体最终停在C点(图中未画出),则BC长度是4m.
点评 解题的关键是:一是弄清楚质点的运动情况,受力和做功情况;二是利用动能定理和机械能守恒列式求解,注意能量间的转化.

练习册系列答案
相关题目
19. 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab的质量为m,导体棒的电阻值R与固定电阻R1、R2的关系为R1=R2=2R,且导体棒与导轨之间的动摩擦因数为μ,导体棒ab由静止沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.则此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab的质量为m,导体棒的电阻值R与固定电阻R1、R2的关系为R1=R2=2R,且导体棒与导轨之间的动摩擦因数为μ,导体棒ab由静止沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.则此时( )
 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab的质量为m,导体棒的电阻值R与固定电阻R1、R2的关系为R1=R2=2R,且导体棒与导轨之间的动摩擦因数为μ,导体棒ab由静止沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.则此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab的质量为m,导体棒的电阻值R与固定电阻R1、R2的关系为R1=R2=2R,且导体棒与导轨之间的动摩擦因数为μ,导体棒ab由静止沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.则此时( )| A. | 电阻R1热功率为$\frac{Fv}{4}$ | B. | 电阻R2热功率为$\frac{Fv}{6}$ | ||
| C. | 整个装置热功率为μmgvcosθ | D. | 导体棒克服摩擦力做功的功率为Fv |
20. 如图所示,一小球静止在光滑半球面上,被竖直放置的光滑挡板挡住.现水平向右缓慢地移动挡板,半球面始终保持静止,则小球缓慢移动到最高点的过程中,挡板对小球的弹力F、半球面对小球的支持力FN的变化情况是( )
如图所示,一小球静止在光滑半球面上,被竖直放置的光滑挡板挡住.现水平向右缓慢地移动挡板,半球面始终保持静止,则小球缓慢移动到最高点的过程中,挡板对小球的弹力F、半球面对小球的支持力FN的变化情况是( )
 如图所示,一小球静止在光滑半球面上,被竖直放置的光滑挡板挡住.现水平向右缓慢地移动挡板,半球面始终保持静止,则小球缓慢移动到最高点的过程中,挡板对小球的弹力F、半球面对小球的支持力FN的变化情况是( )
如图所示,一小球静止在光滑半球面上,被竖直放置的光滑挡板挡住.现水平向右缓慢地移动挡板,半球面始终保持静止,则小球缓慢移动到最高点的过程中,挡板对小球的弹力F、半球面对小球的支持力FN的变化情况是( )| A. | F增大,FN减小 | B. | F增大,FN增大 | C. | F减小,FN减小 | D. | F减小,FN增大 |
4.如图所示,图甲为蹦床比赛中的运动员,图乙为在水平路面上转弯的汽车,图丙为高压带电作业及工作服,图丁为可变电容器.下列与四个图相关的说法中,正确的是( )

| A. | 蹦床对运动员始终存在弹力作用 | |
| B. | 汽车转弯时的向心力由重力提供 | |
| C. | 高压带电作业及工作服中常渗入金属丝 | |
| D. | 可变电容器动片旋入越多电容越小 |
1.高中教材中渗透了许多科学的思维方法,下列说法中正确的是( )
| A. | 根据速度定义式,当△t极小时,就可以表示物体在某时刻的瞬时速度,该定义运用了类比的思想方法 | |
| B. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一段近似看成匀速直线运动,然后把各小段的位移相加,这里运用了等效替代法 | |
| C. | 在研究运动和力的关系时,牛顿做了著名的斜面实验,并运用了理想实验的方法 | |
| D. | 在探究加速度与力、质量之间的关系的实验中,运用了控制变量法 |
18.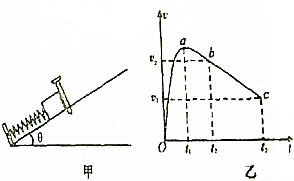 如图甲所示,在倾角为θ的足够长的粗糙斜面底端,一质量m的滑块压缩着一轻弹簧且锁定,但它们并不相连,滑块可视为质点.t=0时解除锁定,计算机通过传感器描绘出滑块的v-t图象如图乙所示,其中Oab段为曲线,bc段为直线,在t2时滑块已上滑距离s以及b、c两点对应的速度v1和v2.已知重力加速度为g,根据图象和题中已知条件( )
如图甲所示,在倾角为θ的足够长的粗糙斜面底端,一质量m的滑块压缩着一轻弹簧且锁定,但它们并不相连,滑块可视为质点.t=0时解除锁定,计算机通过传感器描绘出滑块的v-t图象如图乙所示,其中Oab段为曲线,bc段为直线,在t2时滑块已上滑距离s以及b、c两点对应的速度v1和v2.已知重力加速度为g,根据图象和题中已知条件( )
 如图甲所示,在倾角为θ的足够长的粗糙斜面底端,一质量m的滑块压缩着一轻弹簧且锁定,但它们并不相连,滑块可视为质点.t=0时解除锁定,计算机通过传感器描绘出滑块的v-t图象如图乙所示,其中Oab段为曲线,bc段为直线,在t2时滑块已上滑距离s以及b、c两点对应的速度v1和v2.已知重力加速度为g,根据图象和题中已知条件( )
如图甲所示,在倾角为θ的足够长的粗糙斜面底端,一质量m的滑块压缩着一轻弹簧且锁定,但它们并不相连,滑块可视为质点.t=0时解除锁定,计算机通过传感器描绘出滑块的v-t图象如图乙所示,其中Oab段为曲线,bc段为直线,在t2时滑块已上滑距离s以及b、c两点对应的速度v1和v2.已知重力加速度为g,根据图象和题中已知条件( )| A. | 可以判断滑块在t2时离开弹簧 | |
| B. | 可判断滑块在t3时沿斜面运动到最高点 | |
| C. | 可以求出斜面与滑块之间的动摩擦因数 | |
| D. | 可以求出弹簧锁定时的弹性势能 |
13. 如图所示是一种安装在自行车轮胎边缘用于照明的装置(俗称“电滚子”),内有磁铁与线圈,自行车行驶时,滚轮带着其中的磁体转动,此装置是一个( )
如图所示是一种安装在自行车轮胎边缘用于照明的装置(俗称“电滚子”),内有磁铁与线圈,自行车行驶时,滚轮带着其中的磁体转动,此装置是一个( )
 如图所示是一种安装在自行车轮胎边缘用于照明的装置(俗称“电滚子”),内有磁铁与线圈,自行车行驶时,滚轮带着其中的磁体转动,此装置是一个( )
如图所示是一种安装在自行车轮胎边缘用于照明的装置(俗称“电滚子”),内有磁铁与线圈,自行车行驶时,滚轮带着其中的磁体转动,此装置是一个( )| A. | 自感线圈 | B. | 发电机 | C. | 传感器 | D. | 电动机 |
 将质量为m=1kg的煤块A轻放在以2m/s的恒定速度顺时针转动的足够长水平传送带上后,已知煤块与传送带间动摩擦因数μ=0.05.
将质量为m=1kg的煤块A轻放在以2m/s的恒定速度顺时针转动的足够长水平传送带上后,已知煤块与传送带间动摩擦因数μ=0.05.