题目内容
10.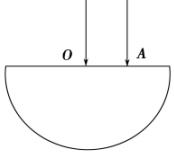 如图所示,半径为R的半圆柱形玻璃砖某一截面的圆心为O点.有两条光线垂直于水平柱面射入玻璃砖中,其中一条光线通过圆心O,另一条光线通过A点,且OA=2R.这两条光线射出玻璃砖后相交于一点,该点到O点的距离为R,求玻璃的折射率.
如图所示,半径为R的半圆柱形玻璃砖某一截面的圆心为O点.有两条光线垂直于水平柱面射入玻璃砖中,其中一条光线通过圆心O,另一条光线通过A点,且OA=2R.这两条光线射出玻璃砖后相交于一点,该点到O点的距离为R,求玻璃的折射率.
分析 画出光路图,根据折射定律和几何关系结合列式,即可求出玻璃的折射率.
解答  解:作出光路图,OBD为法线,则有:
解:作出光路图,OBD为法线,则有:
sin∠ABO=$\frac{OA}{OB}$=$\frac{1}{2}$,∠ABO=30°,
设两条出射光线交点为S,根据几何关系有:
OC=Rcos 30°,
所以,CS=OS-OC=$\frac{\sqrt{3}R}{2}$,
∠BSC=30°,∠SBD=60°,由折射定律:
n=$\frac{sin∠SBD}{sin∠ABO}$=$\frac{sin60°}{sin30°}$=$\sqrt{3}$.
答:玻璃的折射率是$\sqrt{3}$.
点评 画好光路图,理清几何关系,这是解决本题的关键,同时要注意折射定律的应用条件.

练习册系列答案
相关题目
1. 如图甲所示,在倾角为θ的长斜面上有一带风帆的滑块从静止开始沿粗糙斜面下滑,帆受到的空气阻力与滑块下滑的速度成正比,即F=kv,k为已知常数.若滑块从静止开始下滑的加速度a与速度v的关系图象如图乙所示,图中直线的斜率绝对值为b,图中v1为图象与横轴的交点已知,重力加速度为g.则滑块的质量m和动摩擦因数μ为( )
如图甲所示,在倾角为θ的长斜面上有一带风帆的滑块从静止开始沿粗糙斜面下滑,帆受到的空气阻力与滑块下滑的速度成正比,即F=kv,k为已知常数.若滑块从静止开始下滑的加速度a与速度v的关系图象如图乙所示,图中直线的斜率绝对值为b,图中v1为图象与横轴的交点已知,重力加速度为g.则滑块的质量m和动摩擦因数μ为( )
 如图甲所示,在倾角为θ的长斜面上有一带风帆的滑块从静止开始沿粗糙斜面下滑,帆受到的空气阻力与滑块下滑的速度成正比,即F=kv,k为已知常数.若滑块从静止开始下滑的加速度a与速度v的关系图象如图乙所示,图中直线的斜率绝对值为b,图中v1为图象与横轴的交点已知,重力加速度为g.则滑块的质量m和动摩擦因数μ为( )
如图甲所示,在倾角为θ的长斜面上有一带风帆的滑块从静止开始沿粗糙斜面下滑,帆受到的空气阻力与滑块下滑的速度成正比,即F=kv,k为已知常数.若滑块从静止开始下滑的加速度a与速度v的关系图象如图乙所示,图中直线的斜率绝对值为b,图中v1为图象与横轴的交点已知,重力加速度为g.则滑块的质量m和动摩擦因数μ为( )| A. | m=kb | B. | m=$\frac{b}{k}$ | ||
| C. | μ=$\frac{gsinθ+b{v}_{1}}{gcosθ}$ | D. | μ=$\frac{gsinθ-b{v}_{1}}{gcosθ}$ |
18.太阳系中某行星运行的轨道半径为R0,周期为T0,天文学家在长期观测中发现,其实际运行的轨道总是存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离(行星仍然近似做匀速圆周运动).天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星.假设两行星的运行轨道在同一平面内,且绕行方向相同,则这颗未知行星运行轨道的半径R和周期T是(认为未知行星近似做匀速圆周运动)( )
| A. | T=$\frac{{t}_{0}^{2}}{{t}_{0}-{T}_{0}}$ | B. | $R={R_0}\root{3}{{{{(\frac{t_0}{{{t_0}-{T_0}}})}^2}}}$ | ||
| C. | T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0 | D. | R=R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ |
15.如图所示中的几个运动过程中,物体弹性势能增加的是( )
| A. |  跳高运动员从压杆到杆伸直的过程中,杆的弹性势能 | |
| B. |  人拉长弹簧过程中弹簧的弹性势能 | |
| C. |  模型飞机用橡皮筋发射出去的过程中,橡皮筋的弹性势能 | |
| D. |  小球被弹簧向上弹起的过程中,弹簧的弹性势能 |
19.两只不同的弹簧A、B,劲度系数分别为k1、k2,并且k1>k2,现在用相同的力从自然长度开始拉弹簧,当弹簧处于平衡状态时,下列说法中正确的是( )
| A. | A的弹性势能 | B. | B的弹性势能大 | C. | 弹性势能相同 | D. | 无法判断 |
3. 如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )
如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )
 如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )
如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )| A. | vB | B. | $\frac{{v}_{B}}{sinα}$ | C. | vBcotα | D. | vBtanα |
 如图所示一交流发电机的线圈在匀强磁场中匀速转动,线圈匝数N=100,线圈电阻r=3Ω,ab=cd=0.5m,bc=ad=0.4m,磁感应强度B=0.5T,电阻R=311Ω,当线圈以f=5r/s的转速匀速转动时.(π=3.14)
如图所示一交流发电机的线圈在匀强磁场中匀速转动,线圈匝数N=100,线圈电阻r=3Ω,ab=cd=0.5m,bc=ad=0.4m,磁感应强度B=0.5T,电阻R=311Ω,当线圈以f=5r/s的转速匀速转动时.(π=3.14)
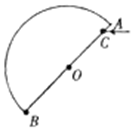 在水平地面上放置着一半径为R的半圆形玻璃砖,直径AB与水平方向的夹角为45°,一束光线从C点水平射入玻璃砖中,OC=$\frac{\sqrt{6}}{3}$R,已知进入玻璃砖的光线第一次到达玻璃砖边缘时,恰好不从玻璃砖射出,求:
在水平地面上放置着一半径为R的半圆形玻璃砖,直径AB与水平方向的夹角为45°,一束光线从C点水平射入玻璃砖中,OC=$\frac{\sqrt{6}}{3}$R,已知进入玻璃砖的光线第一次到达玻璃砖边缘时,恰好不从玻璃砖射出,求: