题目内容
作匀加速直线运动的小车，牵引一条纸带，通过打点计时器，交流电源的频率是50Hz，由纸带上打出的某点开始，每5个点剪下一断纸带，如右图所示，使每一条纸下端与x轴重合，将边与y轴平行，将纸带贴在直角坐标中．求：
①在第一个0.1s内，中间时刻的速度为________．
②运动物体的加速度是________．
0.225m/s 0.75m/s2
分析：使用的方法是等效代替法解题，它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，最后得出结论纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比．
解答：（1）它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，即在第一个0.1s内，中间时刻的速度为：v=
m/s=0.225m/s
（2）
如图所示即相当于物体的速度-时间图象，则斜率即为加速度，横坐标每一纸带的宽度代表0.1s
故：a=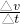
=
m/s2=0.75m/s2
故答案为：0.225m/s，0.75m/s2
点评：纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比．这种等效替代的方法减小了解题难度．
分析：使用的方法是等效代替法解题，它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，最后得出结论纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比．
解答：（1）它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，即在第一个0.1s内，中间时刻的速度为：v=
m/s=0.225m/s（2）
如图所示即相当于物体的速度-时间图象，则斜率即为加速度，横坐标每一纸带的宽度代表0.1s
故：a=
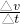=m/s2=0.75m/s2故答案为：0.225m/s，0.75m/s2
点评：纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比．这种等效替代的方法减小了解题难度．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
一个作匀加速直线运动的物体，先后经过a、b两点时的速度分别是v和7v，ab的距离为S，经过ab的时间是t，则下列判断不正确的是（ ）
| A、经过ab中点的速度是5v | ||||
| B、经过ab中间时刻的速度是4v | ||||
C、前
| ||||
D、前
|
如图所示，分别沿倾角不同的斜面由静止向上拉同一个物体，物体与各斜面间的动摩擦因数相同，拉力方向与各斜面均保持平行，物体沿不同斜面作匀加速直线运动的加速度大小均相同，上升的竖直高度也相同．在此过程中（ ）| A、无论沿什么斜面拉，克服摩擦力做的功相同 | B、无论沿什么斜面拉，合外力做的功均相同 | C、沿倾角较大的斜面拉，克服重力做的功较多 | D、沿倾角较小的斜面拉，拉力做的功较多 |