题目内容
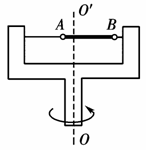
 如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴x和2x处,并用不可伸长的轻绳相连.已知两球与杆之间的最大静摩擦力都是fm.试分析转速ω从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,ω与m、x、fm的关系式.
如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴x和2x处,并用不可伸长的轻绳相连.已知两球与杆之间的最大静摩擦力都是fm.试分析转速ω从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,ω与m、x、fm的关系式.(1)绳中刚出现张力时;
(2)A球所受的摩擦力方向改变时;
(3)两球相对轴刚要滑动时.
分析:角速度从零开始逐渐增大,当较小时,A和B只靠自身静摩擦力提供向心力,当B达到最大静摩擦力时,绳子开始出现张力;绳子出现张力后,角速度增大,张力增大,A球所受的摩擦力减小,当张力达到一定程度时,A球摩擦力反向;当A球摩擦力反向后达到最大静摩擦力时,两球相对轴滑动.
解答:解:(1)角速度从零开始逐渐增大,当较小时,A和B只靠自身静摩擦力提供向心力.B球先达到最大静摩擦力,然后绳子开始出现张力.
有:fm=m?2xω1 2
解得ω1=
.
(2)当绳上出现张力后,角速度增大,张力增大,A球所受的摩擦力减小,当张力达到一定程度时,A球摩擦力反向.
有:fm+T=m?2xω22
T=mxω2 2
联立两式解得ω2=
.
(3)当角速度从x6继续增加时,A球所受的摩擦力方向将沿杆指向外侧,并随ω的增大而增大,直至fA=fm为止.设此时角速度为ω3,并有如下情况:
A球 T-fm=m
x
B球 fm+T=m
2x
解之得 ω3=
若角速度从ω3继续增加,A和B将一起相对轴运动.
答:(1)绳中刚出现张力时ω1=
.
(2)A球所受的摩擦力方向改变时ω2=
.
(3)两球相对轴刚要滑动时ω3=
.
有:fm=m?2xω1 2
解得ω1=
|
(2)当绳上出现张力后,角速度增大,张力增大,A球所受的摩擦力减小,当张力达到一定程度时,A球摩擦力反向.
有:fm+T=m?2xω22
T=mxω2 2
联立两式解得ω2=
|
(3)当角速度从x6继续增加时,A球所受的摩擦力方向将沿杆指向外侧,并随ω的增大而增大,直至fA=fm为止.设此时角速度为ω3,并有如下情况:
A球 T-fm=m
| ω | 2 3 |
B球 fm+T=m
| ω | 2 3 |
解之得 ω3=
|
若角速度从ω3继续增加,A和B将一起相对轴运动.
答:(1)绳中刚出现张力时ω1=
|
(2)A球所受的摩擦力方向改变时ω2=
|
(3)两球相对轴刚要滑动时ω3=
|
点评:解决本题的关键理清A、B球做圆周运动向心力的来源,以及能够通过A、B两球向心力的变化判断出小球受力的变化.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴 和
和 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴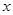 和
和 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴 和
和 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,