题目内容
14. 如图所示,小球被两根细线BA和CD拉住,BA在水平方向,CD跟竖直方向成θ 角,此时CD上的拉力为F1,现将BA剪断,小球开始摆动,当小球返回A点时CD上拉力为F2,则$\frac{{F}_{1}}{{F}_{2}}$为cos 2 θ( 用θ 的函数表示).
如图所示,小球被两根细线BA和CD拉住,BA在水平方向,CD跟竖直方向成θ 角,此时CD上的拉力为F1,现将BA剪断,小球开始摆动,当小球返回A点时CD上拉力为F2,则$\frac{{F}_{1}}{{F}_{2}}$为cos 2 θ( 用θ 的函数表示).
分析 将AB线烧断前,小球处于静止状态,对小球受力分析,根据共点力平衡条件列式求解T1;将AB线烧断,小球开始摆动,当小球返回原处时,速度为零,向心力为零,根据牛顿第二定律求解T2,即可得解.
解答 解:将AB线烧断前,小球处于静止状态,小球受到重力G、AB的拉力TAB和AC的拉力T1.
根据共点力平衡条件得:
竖直方向:T1cosθ=G,得:
T1=$\frac{G}{cosθ}$
将AB线烧断,小球开始摆动,当小球返回原处时,速度为零,向心力为零,根据牛顿第二定律得:
T2-Gcosθ=man=0,
得T2=Gcosθ
故$\frac{{T}_{2}}{{T}_{1}}$=cos2θ
故答案为:cos 2 θ.
点评 本题要抓住两种情况的区别:小球静止时,合力为零;将AB线烧断,小球开始摆动,当小球返回原处时,速度为零,向心力为零,即沿绳子方向的合力为零.

练习册系列答案
相关题目
6.在图左边的实验装置中,铁芯F上绕着两个线圈A、B.如果线圈A中的电流i和时间的关系如图甲、乙、丙、丁所示,在t1~t2这段时间内,对应图甲、乙、丙、丁的那种情况下线圈B中会产生感应电动势( )

| A. | 甲的情况 | B. | 乙的情况 | C. | 丙的情况 | D. | 丁的情况 |
5.一台变压器的原线圈匝数为100,副线圈匝数为1200,在原线圈两端接有电动势为10V的电池组,则在副线圈两端的输出电压为( )
| A. | 0V | B. | 约0.8V | C. | 12V | D. | 120V |
9. 在如图所示电路中,电源电动势为E,内阻为r,电流表A1、A2、电压表V1、V2均为理想电表,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P从最高端向下滑动的过程中( )
在如图所示电路中,电源电动势为E,内阻为r,电流表A1、A2、电压表V1、V2均为理想电表,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P从最高端向下滑动的过程中( )
 在如图所示电路中,电源电动势为E,内阻为r,电流表A1、A2、电压表V1、V2均为理想电表,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P从最高端向下滑动的过程中( )
在如图所示电路中,电源电动势为E,内阻为r,电流表A1、A2、电压表V1、V2均为理想电表,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P从最高端向下滑动的过程中( )| A. | 电流表A1读数先变小后变大,电流表A2读数一直变大 | |
| B. | 电源的输出功率先增大后减小 | |
| C. | 电压表V1示数与电流表A1示数的比值不变 | |
| D. | 电压表V2示数的变化量与电流表A1示数的变化量的比值保持不变 |
19.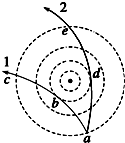 如图所示,虚线为某点电荷电场的等势面,现有两个重力可忽略不计的带电粒子,其比荷相同,二者以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动,图中a、b、c、d、e是粒子轨迹与各等势面的交点,则可以判断( )
如图所示,虚线为某点电荷电场的等势面,现有两个重力可忽略不计的带电粒子,其比荷相同,二者以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动,图中a、b、c、d、e是粒子轨迹与各等势面的交点,则可以判断( )
 如图所示,虚线为某点电荷电场的等势面,现有两个重力可忽略不计的带电粒子,其比荷相同,二者以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动,图中a、b、c、d、e是粒子轨迹与各等势面的交点,则可以判断( )
如图所示,虚线为某点电荷电场的等势面,现有两个重力可忽略不计的带电粒子,其比荷相同,二者以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动,图中a、b、c、d、e是粒子轨迹与各等势面的交点,则可以判断( )| A. | 两个粒子的电性相同 | |
| B. | 经过b、d两点时,两粒子的速率相等 | |
| C. | 经过b、d两点时,两粒子的加速度大小相等 | |
| D. | 经过c、e两点时,两粒子的电势能相等 |
6.关于电磁波的性质和用途,下列说法正确的是( )
| A. | 微波宜用地波传播 | |
| B. | 无线电选台的过程就是调制 | |
| C. | 在广播电视中,声音和图象信号可以利用电磁波传递 | |
| D. | 真空中电磁波的传播速度对不同惯性参考系是不同的 |
4. 如图所示,一带电小球自固定斜面顶端A点以速度v0水平抛出,经时间t1落在斜面上B点.现在斜面空间加上竖直向下的匀强电场,仍将小球自A点以速度v0水平抛出,经时间t2落在斜面上B点下方的C点.不计空气阻力,以下判断正确的是( )
如图所示,一带电小球自固定斜面顶端A点以速度v0水平抛出,经时间t1落在斜面上B点.现在斜面空间加上竖直向下的匀强电场,仍将小球自A点以速度v0水平抛出,经时间t2落在斜面上B点下方的C点.不计空气阻力,以下判断正确的是( )
 如图所示,一带电小球自固定斜面顶端A点以速度v0水平抛出,经时间t1落在斜面上B点.现在斜面空间加上竖直向下的匀强电场,仍将小球自A点以速度v0水平抛出,经时间t2落在斜面上B点下方的C点.不计空气阻力,以下判断正确的是( )
如图所示,一带电小球自固定斜面顶端A点以速度v0水平抛出,经时间t1落在斜面上B点.现在斜面空间加上竖直向下的匀强电场,仍将小球自A点以速度v0水平抛出,经时间t2落在斜面上B点下方的C点.不计空气阻力,以下判断正确的是( )| A. | 小球一定带负电 | |
| B. | 小球所受电场力可能大于重力 | |
| C. | 小球两次落在斜面上的速度方向一定相同 | |
| D. | 小球两次落在斜面上的速度大小可能不同 |
 关于做“测电源电动势和内阻”的实验.某同学通过改变滑动变阻器的电阻,测得了6组U、I的数据,根据第1、2、3、4、5和6组的数据,他在U-I图上标出了这些数据点,并且按照这些数据点的分布绘制了相应的U-I图线[如图所示],由这一图线,可求得电源的电动势E为1.45V,内电阻r为0.5Ω.如果他不利用这一图线,而是利用任意两组U、I数据,那么当他选择哪二组数据求出的E、r值时误差最大?答:2、3(写数据组编号如1和2;3和4;5和6).
关于做“测电源电动势和内阻”的实验.某同学通过改变滑动变阻器的电阻,测得了6组U、I的数据,根据第1、2、3、4、5和6组的数据,他在U-I图上标出了这些数据点,并且按照这些数据点的分布绘制了相应的U-I图线[如图所示],由这一图线,可求得电源的电动势E为1.45V,内电阻r为0.5Ω.如果他不利用这一图线,而是利用任意两组U、I数据,那么当他选择哪二组数据求出的E、r值时误差最大?答:2、3(写数据组编号如1和2;3和4;5和6). 为测出电流表的内阻,采用如图所示的电路原理图,请将以下各实验步骤填写完整.
为测出电流表的内阻,采用如图所示的电路原理图,请将以下各实验步骤填写完整.