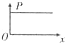题目内容
如图所示，边长为L、匝数为n的正方形金属线框，它的质量为m、电阻为R，用细线把它悬挂于一个有界的匀强磁场边缘．金属框的上半部处于磁场内，下半部处于磁场外，磁场随时间的变化规律为B=kt．已知细线所能承受的最大拉力为2mg，则从t=0开始，经多长时间细线会被拉断？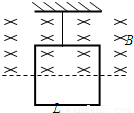
【答案】分析：根据法拉第电磁感应定律求出线圈回路电流方向，然后求出安培力的大小和方向，根据平衡条件进一步求解．
解答：解：根据法拉第电磁感应定律得：
①
②
③
联立①②③解得：
，根据左手定则可知，安培力方向向下．
故当细线承受的最大拉力为2mg时有：
T=2mg=F+mg，将F代人解得：
．
故经过时间
细线会被拉断．
点评：本题考查了电磁感应定律和安培力公式、左手定则、受力平衡等知识点的简单综合应用．
解答：解：根据法拉第电磁感应定律得：
① ② ③联立①②③解得：
，根据左手定则可知，安培力方向向下．故当细线承受的最大拉力为2mg时有：
T=2mg=F+mg，将F代人解得：
．故经过时间
细线会被拉断．点评：本题考查了电磁感应定律和安培力公式、左手定则、受力平衡等知识点的简单综合应用．
练习册系列答案
金钥匙试卷系列答案
相关题目
如图所示，边长为L的正方形区域abcd内存在着匀强电场．电荷量为q、动能为Ek的带电粒子从a点沿ab方向垂直于电场线进入电场，不计重力作用
一质点从如图所示的边长为L的正方形轨道的一个顶点开始沿轨道做匀速率运动，质点运动速率为v，在运动过程中：
如图所示，边长为L的正方形线图abcd匝数为n、电阻为r，外电路的电阻为R，线圈位于磁感应强度为B的匀强磁场中，若线圈从图示位置开始，以角速度ω绕OO′轴匀速转动，则以下判断中正确的是（ ）
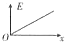
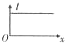
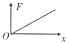
如图所示，边长为L的正方形区域abcd内存在着匀强电场．电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场，不计重力．若粒子从c点离开电场，则电场强度的大小为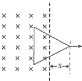
如图所示，边长为L的正三角形闭合金属框架，全部处于垂直于框架平面的匀强磁场中，现把框架匀速拉出磁场，图象中E为回路电动势，I为回路电流，F为所加外力，P为回路电功率，x为框架位移．则框架拉出磁场的过程中，正确的图象是（ ）
