Question

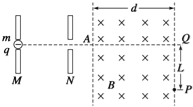
【题目】如图所示，在竖直平面内有水平向左的匀强电场，在匀强电场中有一根长为L的绝缘细线，细线一端固定在O点，另一端系一质量为m的带电小球。小球静止时细线与竖直方向成θ角，此时让小球获得初速度且恰能绕O点在竖直平面内做圆周运动，重力加速度为g。下列说法正确的是( )

A.匀强电场的电场强度E＝

B.小球动能的最小值为Ek＝

C.小球运动至圆周轨迹的最高点时机械能最小

D.小球从初始位置开始，在竖直平面内运动一周的过程中，其电势能先减小后增大

Answer 1

【答案】AB

【解析】

A．小球静止时细线与竖直方向成θ角，受重力、拉力和电场力，三力平衡，根据平衡条件，有：

mgtanθ＝qE

解得

E＝

故A正确；

B．小球恰能绕O点在竖直平面内做圆周运动，在等效最高点A速度最小，拉力为零，根据牛顿第二定律，有：

则最小动能

故B正确；

C．运动过程中小球的机械能和电势能之和不变，则小球运动至电势能最大的位置时机械能最小，小球带负电，则小球运动到圆周轨迹的最左端时机械能最小，故C错误；

D．小球从初始位置开始，若在竖直平面内逆时针运动一周，电场力先做正功后做负功再做正功，则其电势能先减小后增大再减小，同理，若顺时针运动一周，其电势能先增大后减小再增大，故D错误。

故选AB。