题目内容
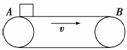
如图4-5-12所示,底座A上装有0.5 m长的直立杆,底座和杆的总质量为M=0.2 kg,杆上套有质量为0.05 kg的小环B,它与杆之间有摩擦.当环从底座上以4 m/s的初速度飞起时,刚好能达到杆顶而没有脱离直立杆,取g=10 m/s2.
求:在环升起过程中,底座对水平面的压力为多大?

图4-5-12
解析:对环进行受力分析:环受重力及杆给环的摩擦力,由牛顿第二定律mg+Ff=ma
环刚好到杆顶,由运动学公式v2=2ax
可得a=16 m/s2 Ff=0.3 N
对底座进行受力分析,底座受重力Mg,水平面的支持力FN和环对杆向上的摩擦力Ff′,由牛顿第三定律Ff=Ff′,由平衡条件
Mg=FN+Ff′,故FN=Mg-Ff′即FN=1.7 N,
又由牛顿第三定律,底座对水平面压力与底座受的支持力等大反向,故底座对水平面压力为1.7 N.
答案:1.7 N
![]()

某同学利用如图4-5-12所示的实验装置验证机械能守恒定律.该同学经正确操作得到打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1、2、3、4、5、6、7,测量各计数点到第一个点的距离h,并正确求出打相应点时的速度v.各计数点对应的数据见下表:
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| h/m | 0.124 | 0.194 | 0.279 | 0.380 | 0.497 | 0.630 | 0.777 |
| v/(m·s-1) |
| 1.94 | 2.33 | 2.73 | 3.13 | 3.50 | |
| v2/(m2·s-2) |
| 3.76 | 5.43 | 7.45 | 9.80 | 12.3 |
请在图4-5-13坐标中,描点作出v2-h图线;由图线可知,重锤下落的加速度g′=________ m/s2(保留三位有效数字);若当地的重力加速度g=9.80 m/s2,根据作出的图线,能粗略验证自由下落的重锤机械能守恒的依据是____________________________________________.

图4-5-12

图4-5-13