题目内容
长为L的轻绳，将其两端分别固定在相距为d的两竖直墙面上的A、B两点．一小滑轮O跨过绳子下端悬挂一重力为G的重物C，平衡时如图所示，求AB绳中的张力．分析：对O点进行受力分析，同一根绳子拉力处处相等，则AO段绳子与 BO段绳子的拉力必然相等．
解答：解：对O点进行受力分析如图：
OA与OB为同一根绳子，故TA=TB
根据平衡条件，水平方向：TA?cosα=TB?cosβ
则cosα=cosβ
即α=β，则AO与BO与水平方向和竖直方向夹角相等．
根据平衡条件，竖直方向：2T?sinα=G
又：d=L?cosα 得cosα=
则sinα=
得：T=
答：绳子上的拉力大小为
．
OA与OB为同一根绳子，故TA=TB
根据平衡条件，水平方向：TA?cosα=TB?cosβ
则cosα=cosβ
即α=β，则AO与BO与水平方向和竖直方向夹角相等．
根据平衡条件，竖直方向：2T?sinα=G
又：d=L?cosα 得cosα=
| d |
| L |
| ||
| L |
得：T=
| GL | ||
2
|
答：绳子上的拉力大小为
| GL | ||
2
|
点评：本题关键是根据几何知识分析α与绳子的长度和两墙壁墙壁距离的关系．
练习册系列答案
习题精选系列答案
相关题目
如图所示，一圆盘可以绕其竖直轴在水平面内运动，圆盘半径为R，甲、乙两物体的质量分别为M和m（M＞m），它们与圆盘之间的最大静摩擦力均为正压力的u倍，两物体用长为L的轻绳连在一起，L＜R．若将甲物体放在转轴位置上，甲、乙连线正好沿半径方向拉直（此时轻绳的拉力为零），若圆盘的角速度缓慢增加，将两物体看作质点．则：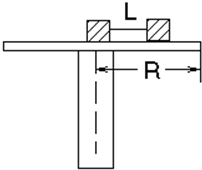
如图所示，一圆盘可以绕其竖直轴在水平面内运动，圆盘半径为R，甲、乙两物体的质量分别为M和m（M＞m），它们与圆盘之间的最大静摩擦力均为正压力的μ倍，两物体用长为L的轻绳连在一起，L＜R．若将甲物体放在转轴位置上，甲、乙连线正好沿半径方向拉直，开始时转盘角速度为零且连线无张且甲、乙物体均可视为质点．现缓慢增大转盘的角速度ω，试求：