题目内容
2. 如图所示,有一种嵌入式照明设备,LED点光源S镶嵌在下层玻璃板内,上层平玻璃板的折射率为n1=$\sqrt{2}$,厚度H1=1cm,下层平玻璃板的折射率n2=2,厚度H2=$\sqrt{3}$cm,点光源发出的光可在空气中大范围看到,还防水防尘,求:
如图所示,有一种嵌入式照明设备,LED点光源S镶嵌在下层玻璃板内,上层平玻璃板的折射率为n1=$\sqrt{2}$,厚度H1=1cm,下层平玻璃板的折射率n2=2,厚度H2=$\sqrt{3}$cm,点光源发出的光可在空气中大范围看到,还防水防尘,求:①光在下层玻璃板内传播的速度;
②要使光在空气中传播的范围最大,上层玻璃板上表面的最小面积为多大?(画出光路图)
分析 ①光在介质中的传播速度由公式v=$\frac{c}{n}$求解;
②A、B点的折射角为90°时光在空气中传播的范围最大,画出光路图,由几何知识得到入射角,由折射定律求出折射角,再结合几何求上层玻璃板上表面的最小面积.
解答  解:①光在下层玻璃板内传播的速度 v=$\frac{c}{{n}_{2}}$=$\frac{3×1{0}^{8}}{2}$=1.5×108m/s
解:①光在下层玻璃板内传播的速度 v=$\frac{c}{{n}_{2}}$=$\frac{3×1{0}^{8}}{2}$=1.5×108m/s
②A、B点的折射角为90°时光在空气中传播的范围最大,画出光路图如图所示.
则 sinθ=$\frac{1}{{n}_{1}}$=$\frac{\sqrt{2}}{2}$,θ=45°
所以n2sinα=n1sinθ,得 sinα=$\frac{{n}_{1}sinθ}{{n}_{2}}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{2}$=$\frac{1}{2}$,α=30°
则 R=r1+r2=2cm
最小面积为 S=πR2=4π cm2;
答:
①光在下层玻璃板内传播的速度为1.5×108m/s.
②要使光在空气中传播的范围最大,上层玻璃板上表面的最小面积为4π cm2.
点评 本题的关键是掌握折射定律和发生全反射时的通式:$\frac{sinC}{sinθ}$=$\frac{{n}_{2}}{{n}_{1}}$,再结合几何知识解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.关于行星绕太阳运动的下列说法中正确的是( )
| A. | 所有行星都在同一椭圆轨道上绕太阳运动 | |
| B. | 行星绕太阳运动时太阳位于行星轨道的中心处 | |
| C. | 离太阳越近的行星的运动周期越短 | |
| D. | 所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等 |
10.如图为同一单摆在两次受迫振动中的共振曲线,下列说法中错误的是( )


| A. | 若两次受迫振动分别在月球上和地球上进行,且摆长相同,则图线Ⅰ表示月球上单摆的共振曲线 | |
| B. | 若两次受迫振动是在地球上同一地点进行,则两次单摆的摆长之比L1:L2=25:4 | |
| C. | 图线Ⅱ若是在地球上完成的,则该摆摆长约为1m | |
| D. | 若摆长均为1m,则图线Ⅰ是在地球上完成的 |
17. 一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )
一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )
 一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )
一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )| A. | 在R上串联一比R小得多的电阻 | B. | 在R上串联一比R大得多的电阻 | ||
| C. | 在R上并联一比R小得多的电阻 | D. | 在R上并联一比R大得多的电阻 |
7. 如图所示为氢原子的能极示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )
如图所示为氢原子的能极示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )
 如图所示为氢原子的能极示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )
如图所示为氢原子的能极示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )| A. | 这群氢原子能发出三处不同频率的光 | |
| B. | 这群氢原子发出光子均能使金属钾发生光电效应 | |
| C. | 金属钾表面逸出的光电子最大初动能一定小于12.09ev | |
| D. | 金属钾表面逸出的光电子最大初动能可能等于9.84ev | |
| E. | 氢原子发出光子后其核外电子动能变小 |
14. 用一激光束照射在云层底面上,云层底面是与地面平行的平面,如图所示,云层底面距地面高h,激光束以匀角速度ω在竖直平面内转动,云层底面上光点( )
用一激光束照射在云层底面上,云层底面是与地面平行的平面,如图所示,云层底面距地面高h,激光束以匀角速度ω在竖直平面内转动,云层底面上光点( )
 用一激光束照射在云层底面上,云层底面是与地面平行的平面,如图所示,云层底面距地面高h,激光束以匀角速度ω在竖直平面内转动,云层底面上光点( )
用一激光束照射在云层底面上,云层底面是与地面平行的平面,如图所示,云层底面距地面高h,激光束以匀角速度ω在竖直平面内转动,云层底面上光点( )| A. | 做匀速圆周运动 | |
| B. | 做变速直线运动 | |
| C. | 当光束转到竖直方向夹角为θ时,光点的移动速度是$\frac{hω}{co{s}^{2}θ}$ | |
| D. | 当光束转到竖直方向夹角为θ时,光点的移动速度是hωtanθ |
11.天文观测中发现宇宙中存在着“双星”.所谓双星,是两颗质量分别为M1和M2的星球,它们的距离为r,而r远远小于它们跟其它天体之间的距离,这样的双星将绕着它们的连线上的某点O作匀速圆周运动.现假定有一双星座,其质量分别为M1和M2,且M1>M2,用我们所学的知识可以断定这两颗星( )
| A. | M1对M2引力比M2对M1的引力大 | B. | M1运动周期比M2运动周期长 | ||
| C. | M1运动半径比M2运动半径小 | D. | M1运动速率比M2运动速率小 |
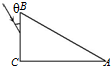 如图所示,一个横截面为直角三角形的三棱镜,∠C=90°.一条与BC面成θ=30°角的光线斜射向BC面,第一次经AC面时即刚好发生全反射.求:该棱镜材料的折射率n.
如图所示,一个横截面为直角三角形的三棱镜,∠C=90°.一条与BC面成θ=30°角的光线斜射向BC面,第一次经AC面时即刚好发生全反射.求:该棱镜材料的折射率n.