Question

如图所示，半径为R的 1/4光滑圆弧轨道最低点D与水平面相切，在D点右侧L₀=4R处用长为R的细绳将质量为m的小球B（可视为质点）悬挂于O点，小球B的下端恰好与水平面接触，质量为m的小球A（可视为质点）自圆弧轨道C的正上方H高处由静止释放，恰好从圆弧轨道的C点切入圆弧轨道，已知小球A与水平面间的动摩擦因数μ=0.5，细绳的最大张力F_m=7mg，重力加速度为g，试求：

（1）若H=R，小球A到达圆弧轨道最低点D时所受轨道的支持力；

（2）试讨论H在什么范围内，小球A与B发生弹性碰撞后细绳始终处于拉直状态。

 

Answer 1

【答案】

（1）5mg（2）或者

【解析】

试题分析：（1）设小球A运动到圆弧轨道最低点D时速度为v₀，则由机械能守恒定律有：

    ①             

圆弧轨道最低点有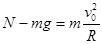：  ②  

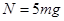解得：     ③

（2）设A与B碰前速度为v_A，碰后A的速度为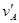，B的速度为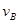，则

A在水平面上滑行过程有：       ④

A与B碰撞过程有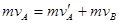：                    ⑤

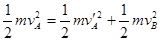              ⑥

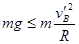①若碰后B能在竖直平面内做完整的圆周运动，则细绳始终处于拉直状态，设小球B在最高处速度为，则在最高处有：  ⑦    

小球B从最低点到最高点有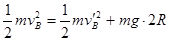： ⑧ 

小球B在最低点时细绳受力最大，则有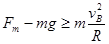：⑨

联立①④⑤⑥⑦⑧⑨解得：           ⑩ 

②若A与B碰后B摆动的最大高度小于R，则细绳始终处于拉直状态，则

根据机械能守恒有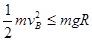：                    ⑾

要保证A与B能发生碰撞，则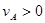                   ⑿

联立①④⑤⑥⑾⑿解得：                  ⒀  

考点：机械能守恒定律、向心力

点评：本题运算过程较复杂，通过向心力公式求绳子拉力，并通过机械能守恒定律结合“发生弹性碰撞后细绳始终处于拉直状态”的具体要求列式求解，本题数学要求较高，属于难题。