题目内容
如图所示，压路机后轮半径是前轮半径的2倍，A、B分别为前轮和后轮边缘上的一点；C为后轮上的一点，它离后轮轴心的距离是后轮半径的一半，则A、B两点的线速度之比为 ，B、C两点的角速度之比为 ．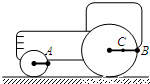
【答案】分析：传动装置，在传动过程中不打滑，则有：共轴的角速度是相同的；同一传动装置接触边缘的线速度大小是相等的．所以当角速度一定时，线速度与半径成正比；当线速度大小一定时，角速度与半径成反比．因此根据题目条件可知三点的线速度及角速度关系．
解答：解：A、B分别为同一传动装置前轮和后轮边缘上的一点，
所以VA=VB，
B、C两点共轴，所以ωC=ωB．
故答案为：1：1；1：1．
点评：本题要紧扣隐含条件：共轴的角速度是相同的；同一传动装置接触边缘的线速度大小是相等的．以此作为突破口；同时能掌握线速度、角速度与半径之间的关系
解答：解：A、B分别为同一传动装置前轮和后轮边缘上的一点，
所以VA=VB，
B、C两点共轴，所以ωC=ωB．
故答案为：1：1；1：1．
点评：本题要紧扣隐含条件：共轴的角速度是相同的；同一传动装置接触边缘的线速度大小是相等的．以此作为突破口；同时能掌握线速度、角速度与半径之间的关系
练习册系列答案
相关题目
如图所示，压路机后轮半径是前轮半径的2倍，A、B分别为后轮和前轮边缘上的一点，C为后轮上的一点．压路机在水平路面上匀速行驶的过程中，A、B两点的线速度始终相等．若用ωA、ωB、ωC分别表示A、B、C三点的角速度，则ωA
如图所示，压路机后轮半径是前轮半径的2倍，A、B分别为前轮和后轮边缘上的一点；C为后轮上的一点，它离后轮轴心的距离是后轮半径的一半，则A、B两点的线速度之比为
如图所示，压路机后轮半径是前轮半径的3倍，A、B分别为前轮和后轮边缘上的一点，C为后轮上的一点，它离后轮轴心的距离是后轮半径的一半，则A、B、C三点的角速度之比
如图所示，压路机后轮的半径是前轮半径的两倍，M为前轮边缘上的一点，N为后轮上一点，它离后轮轴的距离是后轮半径的一半，则M、N的角速度之比为（ ）| A、4：1 | B、2：1 | C、1：1 | D、1：2 |
如图所示，压路机后轮的半径是前轮半径的两倍，M为前轮边缘上的一点，N为后轮上一点，它离后轮轴的距离是后轮半径的一半，则M、N的线速度之比为