题目内容
 (2009?武汉一模)如图所示,一质量为m的物块A与直立的轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为m的物块叠放在A的上面,A、B处于静止状态.若A、B粘连在一起,用一竖直向上的拉力缓慢上提B,当拉力的大小为
(2009?武汉一模)如图所示,一质量为m的物块A与直立的轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为m的物块叠放在A的上面,A、B处于静止状态.若A、B粘连在一起,用一竖直向上的拉力缓慢上提B,当拉力的大小为| mg | 2 |
(1)恒力F的大小;
(2)A与B分离时的速度大小.
分析:(1)当A、B粘连在一起,当拉力的大小为
时,A物块上升的高度为L,结合共点力平衡求出弹簧弹力的大小,当A、B不粘连,在恒力F作用下,恰好分离时A、B的加速度相同,根据牛顿第二定律,对整体和B分别研究,求出恒力F的大小.
(2)当A、B粘连在一起时,根据动能定理求出弹力做功的大小,不粘连时,再对AB整体研究,根据动能定理求出速度的大小.
| mg |
| 2 |
(2)当A、B粘连在一起时,根据动能定理求出弹力做功的大小,不粘连时,再对AB整体研究,根据动能定理求出速度的大小.
解答:解:(1)设弹簧劲度系数为k,A、B静止时弹簧的压缩量为x,则:
x=
…①
A、B粘连在一起缓慢上移,以AB整体为研究对象,当拉力为
时
+k(x-L)=2mg…②
A、B不粘连,在恒力F作用下,恰好分离时,根据牛顿第二定律:
F+k(x-L)-2mg=2ma…③
恰好分离时AB之间的作用力为0,以B为研究对象,根据牛顿第二定律:
F-mg=ma…④
联立方程①②③④解得:F=
mg…⑤
(2)A、B粘连在一起缓慢上移L,设弹簧弹力做功为W弹,根据动能定理;
W+W弹-2mgL=0…⑥
在恒力F的作用下,设A、B分离时的速度为v,根据动能定理:
FL+W弹-2mgL=
?2mv2…⑦
联立方程⑤⑥⑦解得:v=
…⑧
答:(1)恒力F的大小F=
mg.
(2)A与B分离时的速度大小v=
.
x=
| 2mg |
| k |
A、B粘连在一起缓慢上移,以AB整体为研究对象,当拉力为
| mg |
| 2 |
| mg |
| 2 |
A、B不粘连,在恒力F作用下,恰好分离时,根据牛顿第二定律:
F+k(x-L)-2mg=2ma…③
恰好分离时AB之间的作用力为0,以B为研究对象,根据牛顿第二定律:
F-mg=ma…④
联立方程①②③④解得:F=
| 3 |
| 2 |
(2)A、B粘连在一起缓慢上移L,设弹簧弹力做功为W弹,根据动能定理;
W+W弹-2mgL=0…⑥
在恒力F的作用下,设A、B分离时的速度为v,根据动能定理:
FL+W弹-2mgL=
| 1 |
| 2 |
联立方程⑤⑥⑦解得:v=
|
答:(1)恒力F的大小F=
| 3 |
| 2 |
(2)A与B分离时的速度大小v=
|
点评:本题考查了动能定理和牛顿第二定律的综合运用,知道A、B分离的瞬间加速度相同,A、B间的作用力为零.

练习册系列答案
相关题目
 (2009?武汉一模)如图所示,边长为L的等边三角形ABC为两有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计).若从A射出的粒子
(2009?武汉一模)如图所示,边长为L的等边三角形ABC为两有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计).若从A射出的粒子
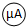 :量程0~200μA、内阻500Ω
:量程0~200μA、内阻500Ω 改装成一个量程略大于2.5V的伏特表,将改装表的电路图画在图甲的方框内,此伏特表
改装成一个量程略大于2.5V的伏特表,将改装表的电路图画在图甲的方框内,此伏特表 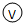 的量程是
的量程是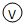 和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线
和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线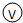 的示数为1.5V,则通过小灯泡的电流强度为
的示数为1.5V,则通过小灯泡的电流强度为